問 題
図のように一様な弾性体の棒の両端ABが壁に固定されている。
この棒の点Cに図に示す方向に軸方向荷重Pが作用するとき、端Aにおける軸方向反力の大きさとして最も妥当なのはどれか。
ただし、棒の長さはlとし、自重は無視する。
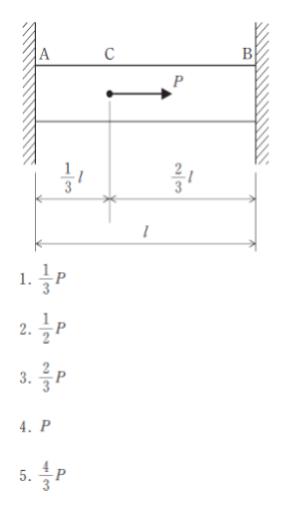
正解 (3)
解 説

上図のように2つに分けて考える。すると、ACの伸び = BCの縮み のはずである。
※RA,RBの方向についてですがACは「伸びる」、CBは「縮む」ように見えることからRAは左向きで、RBも左向き としています。
RA+RB = P です。・・・(1)
また、伸びは、断面積を A 、ヤング率をEとすれば
σAC=RA・(1/3 l)/AE 及び
σCB=RB・(2/3 l)/AE と表すことができます。
この2つが等しいのだから
RA = 2RB となる。・・・(2)
(1)、(2)より
RA = 2/3 P です。
以上より、正解は 3 です。

コメント