問 題
区間0≦x≦2πにおいて、二つの曲線y=sinx、y=cosxのみで囲まれた部分の面積はいくらか。
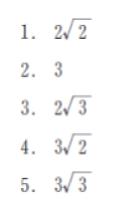
正解 (1)
解 説
【解法1:積分で計算】
y=sinx,y=cosx のグラフを書くと、以下のようになります。求めたいのは、斜線部です。
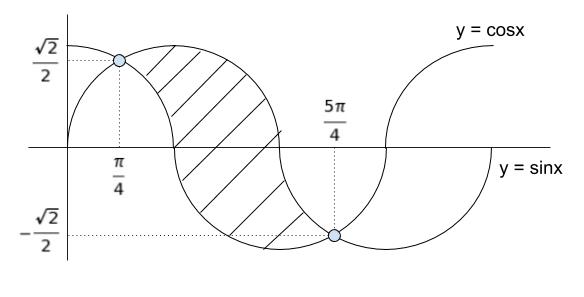
斜線部の面積は定積分の形で表すと以下のようになります。
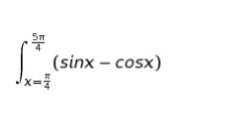
∫ sinx = ーcosx、∫ cosx = sinx なので、計算すると以下のようになります。

まとめると2√2 です。
正解は 1 です。
【解法2:面積評価】
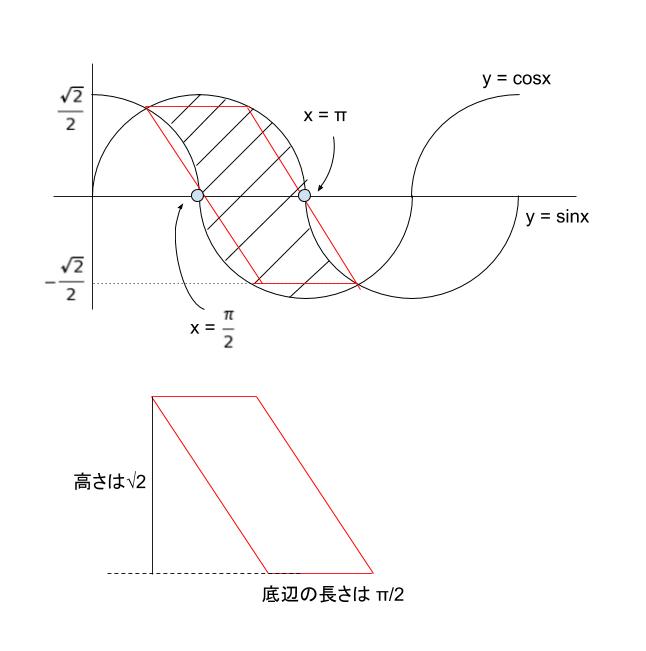
上図のような平行四辺形に注目します。この平行四辺形は、求める面積よりわずかに小さい面積です。
√2 ≒ 1.41 です。π ≒ 3.14 なので、π/2 ≒ 1.57 です。1.41 × 1.57 ≒ 2.2 です。
一番近いのは 選択肢 1 です。
もう少し詳しく見るのであれば、上下に出っ張っている部分を三角形に近似します。
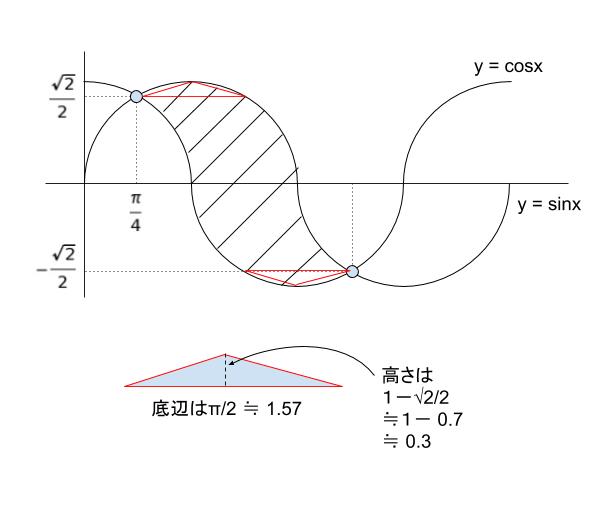
一つの三角形の面積は
1/2 × {1.57 × 0.3}
≒ 1/2 × 0.47
≒ 0.23 ぐらい。
せいぜい 0.25 と見て、それが 2倍で 0.5です。
先程近似した平行四辺形にこの 0.5 を加えても大体 2.7 なので、やはり選択肢 1 が妥当と考えられます。

コメント