問 題
1~100の異なる数字が一つずつ書かれた100枚のカードがあり同じ数字がカードの表・裏両面に書かれている。いま全てのカードが表面を上にして並んでいるところから初めに6の倍数が書かれたカードを全て反対の面に返した。
次にその状態から4の倍数が書かれたカードを全て反対の面に返したとき表面を上にしているカードは何枚か。
1. 41枚
2. 59枚
3. 63枚
4. 67枚
5. 75枚
正解 (5)
解 説
これはいいひっかけ!というのが正直な感想の問題です。初めて解いた時、正解は 4 と飛びついてしまいました。
まず、6の倍数は 100 ÷ 6 = 16 ・・・4で、16 枚裏になります。
次に、4の倍数は 100 ÷ 4 = 25 です。ところが 12 の倍数は、既に一回ひっくり返っているため、表に戻ります。100 ÷ 12 = 8 ・・・4です。
従って、求める枚数は
100ー16ー(25ー8×2)=75 です。
12の倍数については、裏が表になるから、×2をする必要があります。
正解は 5 です。
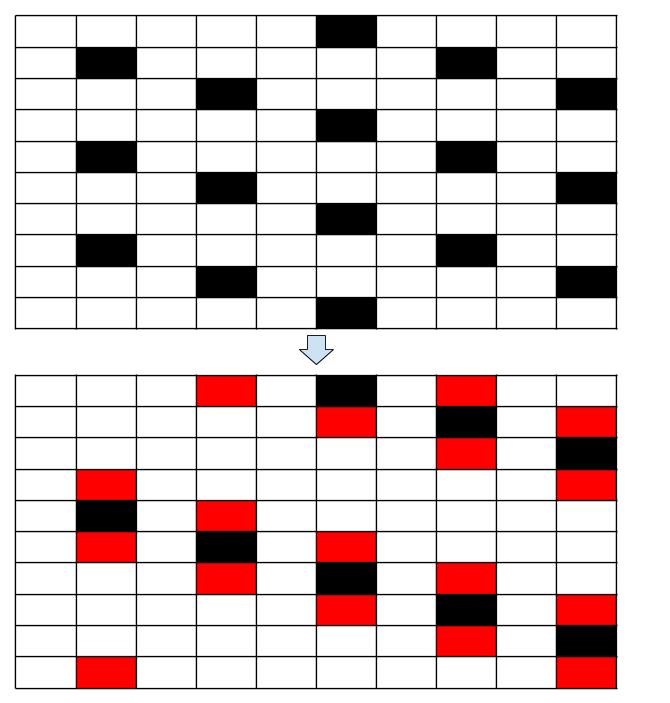
納得いかないかもしれませんので、具体的に書いておきます。10×10のマス目で、6の倍数を黒く塗って、4の倍数を赤く塗り、両方かぶる所の色は透明にもどしたものが下図です。下図で色が塗られている所は 25 マスであることが確認できると思います。

コメント