問 題
A~Eの5人に目隠しをし白又は赤の帽子をかぶせた。帽子の正面には1~5のそれぞれ異なる数字が一つだけ書かれている。目隠しを外し自分以外の4人がかぶっている帽子についてA~Dが次のように述べているとき確実にいえるのはどれか。
A:「白、赤の帽子をかぶっている者がそれぞれ2人おり白の帽子に書かれた数字の和は5である。」
B:「白、赤の帽子をかぶっている者がそれぞれ2人おり白の帽子に書かれた数字の和と赤の帽子に書かれた数字の和は等しい。」
C:「4人の帽子に書かれた数字の和は11である。」
D:「白の帽子をかぶっている者が3人いる。また赤の帽子をかぶっている者が1人おりその帽子に書かれた数字は5である。」
- Aは数字の2が書かれた白の帽子をかぶっている。
- Bは数字の1が書かれた白の帽子をかぶっている。
- Cは数字の4が書かれた赤の帽子をかぶっている。
- Dは数字の3が書かれた赤の帽子をかぶっている。
- Eは数字の2が書かれた白の帽子をかぶっている。
解 説
色、数字についての情報を分けて考えます。まず、色だけに注目します。
A から見て、白、赤、2人ずつ→「B,C,D,E の中に 白2、赤2」とわかります。同様に、B から見て、白、赤、2人ずつ→「A,C,D,E の中に白2、赤2」です。A と B を入れ替えても白、赤の数に変化がないため、A,B は 同じ色の帽子をかぶっています。
D から見て、白3人、赤1人(数字は5)→「A,B,C,E の中に白3、赤1」です。B,C,D,E だと 白2,赤2 だったのだから、A と D を入れ替えて白が1減り、赤が1増えています。従って、A 白(A,B同じ色なので、B も白)、D 赤です。C,E のうちどちらかが白、どちらかが赤の5をかぶっています。
ここまでを表にまとめると以下のようになります。
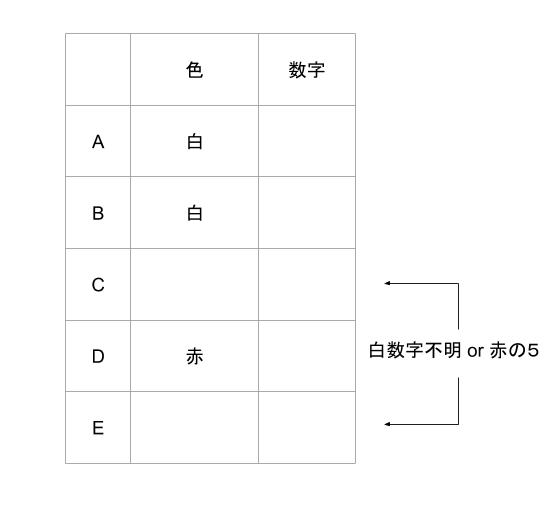
次に数字に注目します。 まず、Aの発言です。「A から見て、白の数字の和が5」ということは、「1と4」か「2と3」の組み合わせとわかります。適当に B を白1と決めつけてみます。すると、C or E のかぶっている白の帽子が白4のはずです。
次に、B の発言に注目します。B から見える赤の帽子の数のうち1個は5です。残っている数は2と3なので、「白の数字の和と、赤の数字の和が等しい」のなら、Dの赤帽子の数は2で、A の帽子は白3のはずです。
すると、C からみたA,B,D,E の数は3,1,2,?です。「和が11」なので、Eの帽子は5です。5ということは赤です。一例として、以下のような組み合わせが OK とわかりました。
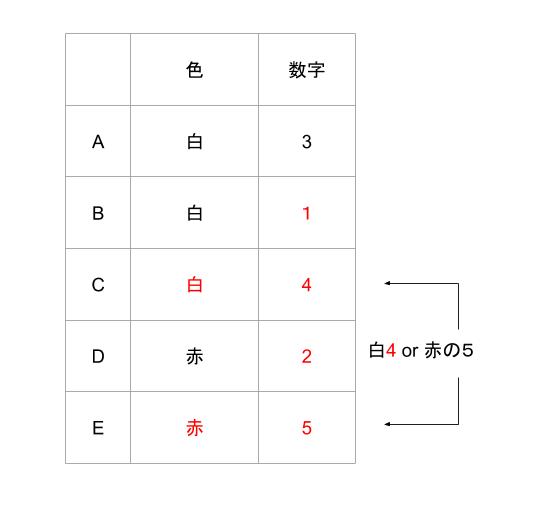
選択肢 を検討すると
選択肢 1 は、数字が違います。
選択肢 2 は、妥当です。
選択肢 3 は、色が違います。
選択肢 4 は、数字が違います。
選択肢 5 ですが、色も数字も違います。
以上より、正解は 2 です。

コメント