公務員試験 H26年 国家一般職(化学) No.11解説

　問 題　　　　　

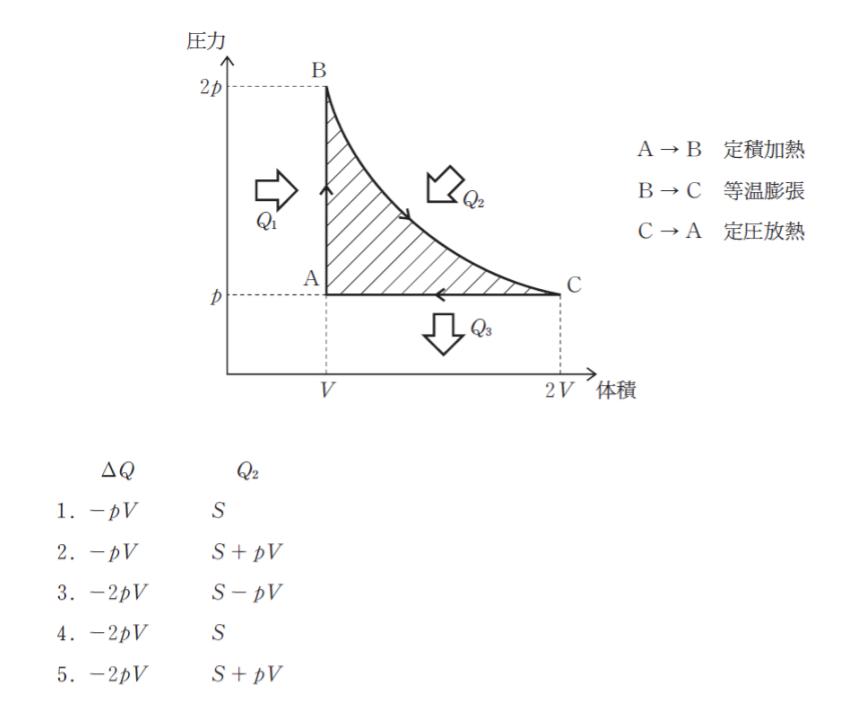
図のように一定量の理想気体を変化させるとき、ΔQ =  Q₁－ Q₃ 及び Q₂ の組合せとして最も妥当なのはどれか。

ただし、図の斜線部の面積を S とする。また定積加熱過程(状態A → B)において気体が受け取る熱量を Q₁、 等温膨張過程(状態 B → C )において気体が受け取る熱量を Q_2、定圧放熱過程(状態 C → A )において気体が放出する熱量を Q₃ とする。

 

 

 

 

 

　解 説　　　　　

気体の仕事、熱　に関する基本公式は以下の 2 つです。「気体、熱、仕事」といった単語が複数問題文に出てきたら、思い出します。

基本公式１：W = pΔV
基本公式２：ΔU = W + Q
※ W は、work の頭文字。仕事を表します。
※ W は、気体が「外から受けた」仕事（例：ギューっと押される　とか）　です。そのため、気体が仕事をした場合は符号が負であることに注意です！
※ ΔU は、気体の持つ内部エネルギーの差です。
※ Q は、気体が外部から受け取る熱　です。

状態　A→B、B→C、C→A　をそれぞれ検討してみます。
 
『 状態 A → B 』
「定積」とあるから ΔV = 0 。つまり、公式 W = pΔV より、W も 0 です。熱は受け取っており、気体の持つ内部エネルギーは変化します。その変化を ΔU とおくと ΔU = Q₁ と表すことができます。
 
『 状態 B → C 』
等温膨張です。つまり、ΔU = 0 です。体積が V → 2V となっているため ΔV が存在する。つまり、W がある。言い換えると、気体が仕事したといえます。

どれくらい仕事したかというのは「PΔV　を、V=V から、V = 2V まで積分」すればわかるのですがこれは、まさに P-V グラフにおいて「B→C の曲線と x 軸で囲まれた部分の面積を求める」　ということです。（ここは、覚えている人も多いと思います。「P－V　グラフなら、面積が仕事」です。）

よって B → C の「気体が外部にした仕事」は、－（S＋PV）　と表すことができます。従って、 0 = －（S + PV） + Q₂ ∴ Q₂ = S + PV です。正解は、2 か 5 に絞られます。
 
『状態 C → A 』
「定圧」なので、P は一定です。この間の仕事は、PV です。従って、公式から ΔU = PV – Q₃
※ 体積が 2V → V になっているため、外部から受ける仕事　となり、PV の符号は正にしています。
※ 図の中で Q₃ が出て行く方向になっているため符号はマイナスにしています。

A→B の内部エネルギー変化が　ΔU（A→B）
B→C は、内部エネルギー変化なし。
C→A の内部エネルギー変化が、ΔU（C→A）であり、結果として全く同じ状態である A に戻っていることから、ΔU（A→B）と、ΔU（C→A）は、合わせると 0 だったと考えられます。

よって
ΔU（A→B）＋ΔU（C→A）
=Q₁ + (PV － Q₃) = 0
つまり、Q₁ － Q₃　= －PV　です。

以上より、正解は 2 です。