公務員試験 H26年 国家一般職(教養) No.21解説

　問 題　　　　　

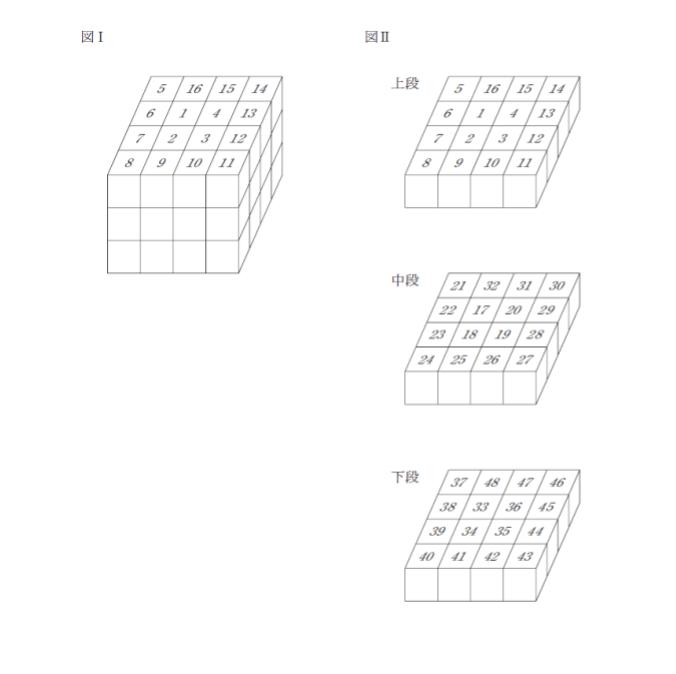
図Ⅰは一辺の長さが１cm の立方体 48 個を隙間なく積み重ねた立体を示したものである。図に示すとおり各立方体には番号が付いており図Ⅰの状態から立方体を１番から順に一つずつ取り除き残った立体の表面積について考える。

15番までの立方体を取り除いたときに残った立体の表面積とｎ番(ただしn ≠ 15)までの立方体を取り除いたときに残った立体の表面積が等しくなるときのｎについて確実にいえるのはどれか。

1. ｎは17のみである。
2. ｎは23のみである。
3. ｎは31のみである。
4. ｎに当てはまる全ての数値の和は40である。
5. ｎに当てはまる全ての数値の和は78である。

 

 

 

 

 

　解 説　　　　　

選択肢 より、 n = 17 の所がわかれば正解がかなり絞れます。

n = 17 まで取り除いた状態は、上段が完全に取り除かれて、内側の立方体が 1 個だけポコッと取り除かれた状態です。いきなりこの状態はよくわからないので、具体的に n = 1 から取り除き、表面積がどのように変化していくかを考えていきます。

n = 1 の立方体を除くと、「もともと１面だけ表面に出ていた」→「残りの５面は、他の立方体の面と接していたために見えなかった」→「５面が見えるようになる」→「－１＋５で、表面積は +4」とわかります。

以下、取り除かれる立方体の何面が表面に出ているかを追うことで、表面積がどう増減するかをまとめていくと、以下の表のようになります。

（個人的には、 n = 6 の所が見逃しやすかったです。 n = 1 の面が既に取り除かれているため、他の面と接しているのは下と n = 7 の立方体の面　の２つしかないんですが、図Ⅰを見ていると、n = 1 の立方体がまだあるような気がして、あれ、表面積全然減っていかない・・・と戸惑いました。）

n	表面に出ている面	表面積の増減
1	1	－１＋５=＋４
2	2	－２＋４=＋２
3	2	－２＋４=＋２
4	3	－３＋３=± ０
5	3	－３＋３=± ０
6	4	－４＋２=－２
7	4	－４＋２=－２
8	4	－４＋２=－２
9	4	－４＋２=－２
10	4	－４＋２=－２
11	4	－４＋２=－２
12	4	－４＋２=－２
13	4	－４＋２=－２
14	4	－４＋２=－２
15	4	－４＋２=－２
16	5	－５＋１=－４

１段目と２段目の表面積の増減は同じため、 n = 17 の時に加え、n = 23 の時にちょうど n = 15 の時と同じ表面積になることがわかります。そこからずっと表面積は減って、多少上がっても、n = 15 の時の表面積まではもどらないため、 n = 17,23 が題意を満たす n です。

従って、正解は 4 です。