公務員試験 H26年 国家一般職(教養) No.13解説

　問 題　　　　　

ある地域における世帯の年収と住居の状況について次のことが分かっているとき確実にいえるのはどれか。

• 年収が500万円以上である世帯数は82世帯、500万円未満である世帯数は56世帯である。
  
• 住居の広さが70平米以上である世帯数は70世帯、70平米未満である世帯数は68世帯である。
  
• 年収が500万円未満で住居の広さが70平米未満である世帯のうち、持家である世帯数は、持家でない世帯数より３世帯多い。
  
• 年収500万円未満の持家でない世帯で、住居の広さが70平米以上である世帯数は12世帯である。
  
• 年収が500万円未満で持家である世帯数は25世帯である。
  
• 年収500万円以上の持家でない世帯のうち住居の広さが70平米未満である世帯数は17世帯で70平米以上である世帯数より９世帯少ない。

1. 持家である世帯数と持家でない世帯数の差は６世帯である。
2. 住居の広さが70平米以上で年収500万円以上の持家でない世帯数は29世帯である。
3. 住居の広さが70平米以上で年収500万円未満の持家である世帯数は12世帯である。
4. 住居の広さが70平米以上の世帯のうち年収500万円未満で持家である世帯数は年収500万円以上で持家である世帯数のちょうど10分の１である。
5. 年収500万円以上で持家である世帯のうち住居の広さが70平米以上の世帯数は70平米未満の世帯数より19世帯多い。

 

 

 

 

 

　解 説　　　　　

• １：年収 500 万円以上、未満
  
• ２：70m2 以上、未満
  
• ３：持家 or そうでないか

という３つの条件による分類なので、ベン図で条件を整理し、式をいじくって考えます。ベン図を書く時、 h の部分を忘れないように気をつけます。

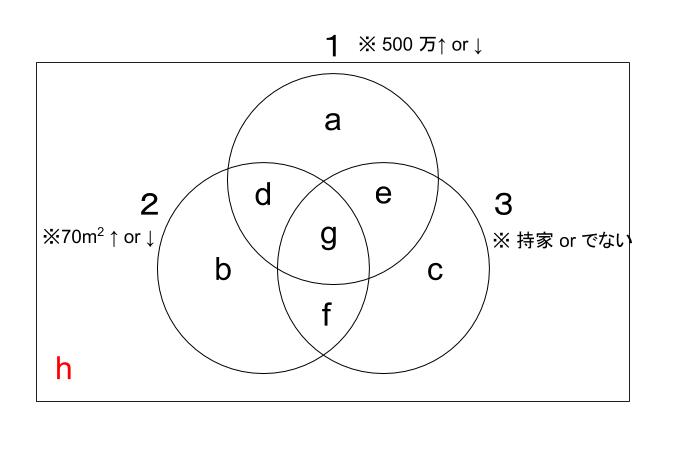
条件を１つ１つ式に直すと

・「500万↑ 82、500万↓ 56」 は
a + d + e + g = 82, b + c + f + h = 56 です。

・「70m²↑ 70、70m²↓ 68」は
b + d + f + g = 70, a + c + e + h = 68 です。

・「500万↓ かつ 70m²↓ のうち、持家が、持家でないより 3 多い」
c = h+3 です。

・「500万↓ かつ 持家でない、で、70m²↑ が 12」
b = 12 です。

・「500万↓ かつ 持家、25」
c + f = 25 です。

・「500万↑ かつ 持家でないのうち、70m²↓が17、70m²↑ よりも９少ない」
a = 17,d = 26 です。

a,b,c,d,e,f,g,h のうち、a,b,d はわかっています。後は式を解いていけばいいのですが、一例として以下のように解くことができます。

c = h+3 と c + f = 25 より、代入することで f + h = 22 とわかります。

すると b+c+f+h = 56 という式より、b = 12,f+h = 22 から、c = 22 とわかります。
c がわかると f = 3,h = 19 です。

a,b,c,d,f,h がわかったので、例えば b+d+f+g = 70 に b = 12,d = 26,f = 3 を代入して、g = 29 です。すると e = 10 とわかります。

まとめると

a = 17,b = 12,c = 22,d = 26、e = 10,f = 3,g = 29,h = 19 です。

選択肢を a~h を用いて書き直すと

• 選択肢 1：c+e+g+g と a+b+d+h の差は 6 ?
  
• 選択肢 2 ：d = 29 ?
  
• 選択肢 3 ：f = 12 ?
  
• 選択肢 4：f = g×10 ?
  
• 選択肢 5 ：g = e+19 ?　です。

選択肢を１つずつ確認すれば、正解は 5 です。