問 題
A~Fの6人が3対3に分かれてバスケットボールの試合を行うためチーム分けをした。チーム分けの方法は6人が一斉にグー又はパーを出し出されたものが同数になるまで繰り返し同数になったとき出したものが同じ者どうしが同じチームになるものとしその結果4回目でチームが決まった。
チーム分けについて各人が次のように述べているとき確実にいえるのはどれか。
A:「3回目まで毎回少数派であった。最終的にはDと同じチームになった。」
B:「2回目以降はその前の回と異なるものを出した。最終的にはEと同じチームになった。」
C:「3回目まで毎回多数派であった。」
D:「3回目まで毎回同じものを出し4回目はこれまでと異なるものを出した。」
E:「2回目で私と同じものを出した者は私以外に3人いた。」
F:「2回目以降はその前の回で少数派であったものを出した。」
- AとEが同じものを出した回はなかった。
- CとFが同じものを出した回は3回あった。
- 4回とも同じものを出した者は1人いた。
- 1回目は多数派5人と少数派1人に分かれた。
- 3回目は多数派5人と少数派1人に分かれた。
解 説
いわゆるグッパーでのチーム分けです。A~Fのどの発言を見ても、誰が何回目にグー or パーを出したと確定できる発言はありません。
そこで、1つ確定すると一気に 1~4回目が確定する点に注目して、Dが1~3回目までで出していたものをとりあえずグーと仮定します。Dはグー、グー、グー、パーと出したと仮定するということです。
すると、最終的に D と同じチームになった 「A」 の「4回め」は パー、「B,E」の「4回め」は グーと確定します。さらに B の「ずっと前の回と異なるものを出していた」という発言から、「B は パー、グー、パー、グー」と出したと決まります。ここまでを表にまとめると以下のようになります。
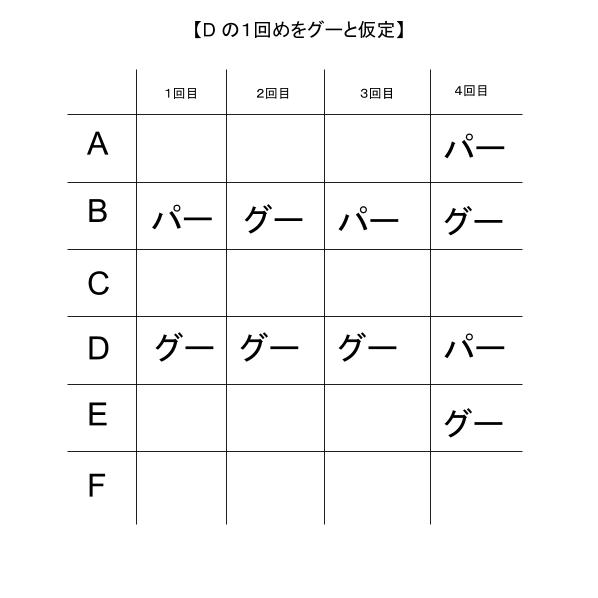
多数派や少数派という発言があったため、グーが既に2人確定している 2回目に注目します。A は 3回目まで少数派であった→2回目も少数派ということから、パーが確定します。また、Cは多数派なので、この時点で グーと確定します。
さらに、2回目に E と同じものを出した者が3人いるのだから、E も多数派、つまりグー です。残った F はパーを出しています。そして、F の発言から、3回目の F が出したのは 2回目の少数派であるパーです。表に追加すると、以下のようになります。
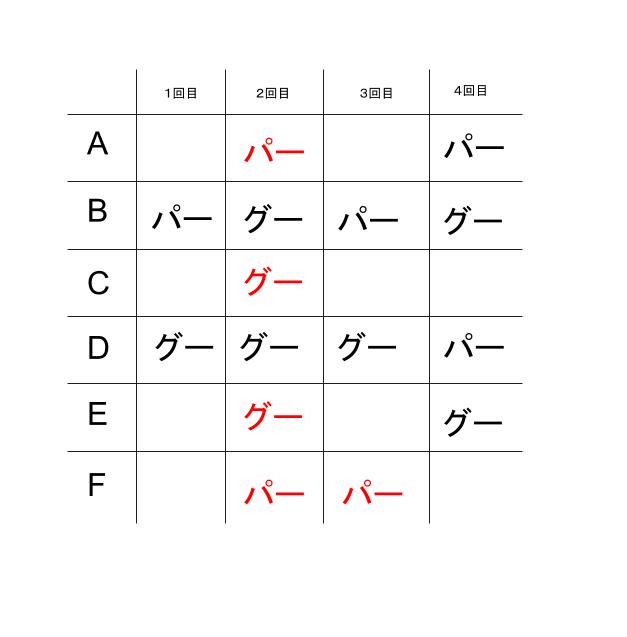
3回目も、2回目と同様に、A は少数派なので、グーです。Cは多数派なので、パーです。残った E はパーでなければ、3回目でグループ分けが決まってしまいます。3回目の少数派が グーなので、4回目のF はグー、残った 4回目の C はパーです。
最後に、少し見つけにくい所かもしれませんが、2回目にFがパーを出しているため、1回目の少数派はパーです。従って、1回目の A は少数派なのでパー、Cは多数派なので、グーです。パーが少数派となるには、残りのE,Fはグーでなければいけません。以下のように確定します。
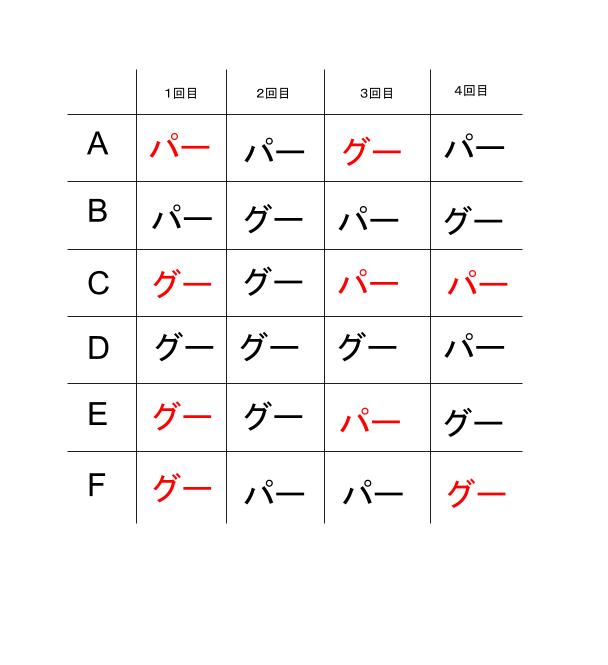
以上より、選択肢を検討すると、選択肢 1 が正しいです。
A と E は常に違う手を出しています。正解は 1 です。

コメント