問 題
ある個人の効用関数が、u = c1 ・c2 で与えられているとする。ただし、u は効用水準、c1 は今期の支出額、c2 は来期の支出額である。
また今期と来期それぞれの予算制約式は、c1 = y1 - S、c2 = (1+ r)S + y2 である。ただし、y1 は今期の所得、y2 は来期の所得であり、S は正であれば貯蓄、負であれば借入れの大きさで、r は市場の利子率である。
いま y1 が120、y2 が 84 であることが分かっていて貯蓄や借入れが市場の利子率5% (r= 0.05) で可能であるとする。このときこの個人が効用を最大化するための行動として妥当なのはどれか。
1. 借入れを 20 だけ行う。
2. 借入れを 15 だけ行う。
3. 貯蓄も借入れも行わない。
4. 貯蓄を 15 だけ行う。
5. 貯蓄を 20 だけ行う。
解 説
C1 を x、C2 を y とします。効用関数は u(x,y) = xy と表すことができます。x = 120 – S、y = 1.05 S + 84 の時、xy の最大を考えるという問題です。y = 1.05 S + 84 を、効用関数の式に代入すると、u(S) = (120 – S)(1.05 S + 84) という、S に関する二次式になります。
解法1
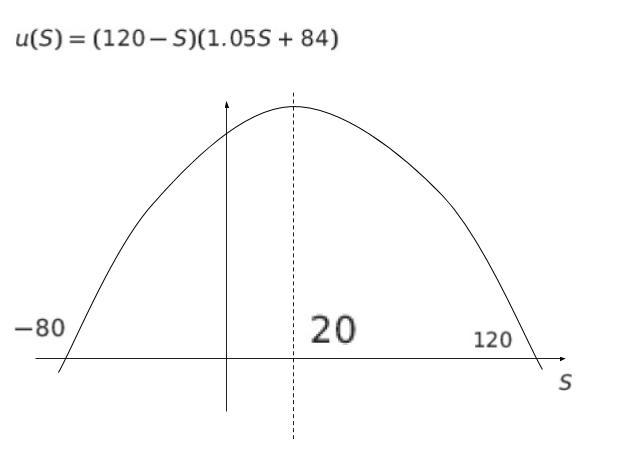
前問題 H26no31 と同様に、u(S) = (120 – S)(1.05 S + 84) のグラフを書きます。S = ー80 と、S = 120 の時、x 軸と交わるような、上に凸の二次関数のグラフです。以下のようになります。S = 20 の時最大です。「貯蓄を 20 行う」とわかります。
解法2
まず、u(S) = (120 – S)(1.05 S + 84) の右辺を展開して、降べきの順に整理します。u(S) = -1.05 S2 +42S +120・84 です。最大値がわかればよいので、S で微分します。u’(S) = -2.1S + 42 です。最大値は u’(S) = 0 の時です。従って、S = 20 の時、最大値をとります。「貯蓄を 20 行う」とわかります。
以上より、正解は 5 です。

コメント