公務員試験 H26年 国家一般職(土木) No.31解説

　問 題　　　　　

宅地を造成するに当たり、対象地を面積の等しい長方形に分割して、これらの長方形の各頂点における地盤高を測量したところ、図に示すとおりであった。

この対象地を切取り土量と盛土量が等しくなるように地ならしして、平坦な土地とする。

地ならし後における土地の地盤高として最も妥当なのはどれか。

ただし、切取り土と盛土の密度は等しいものとし、計算に当たっては、図に示す面積の等しい長方形に分割して点高法により土量を求めるものとする。

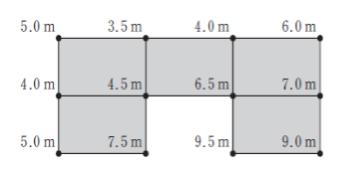
1. 5.6m
2. 5.7m
3. 5.8m
4. 5.9m
5. 6.0m

 

 

 

 

 

　解 説　　　　　

「面積の等しい長方形に分割して点高法」と来れば以下の１，２，３の手順で計算です。

１：分割した長方形の個数を数える。

２：各頂点がいくつの長方形に共通するか数えて Σh₁,Σh₂,Σh₃,Σh₄ を計算する。

※ Σh₁ とは、h₁ の和です。h₁とは「一つの長方形のみに含まれる頂点高さ」です。

Σh₂は、h₂ の和です。h₂=「二つの長方形に共有される頂点高さ」です。

以下、h₃,h₄ も同様に考えます。

３：H = （1×Σh₁＋2×Σh₂＋3×Σh₃＋4×Σh₄）/  (個数×4)

本問では

１：分割した長方形の個数は「５」個。

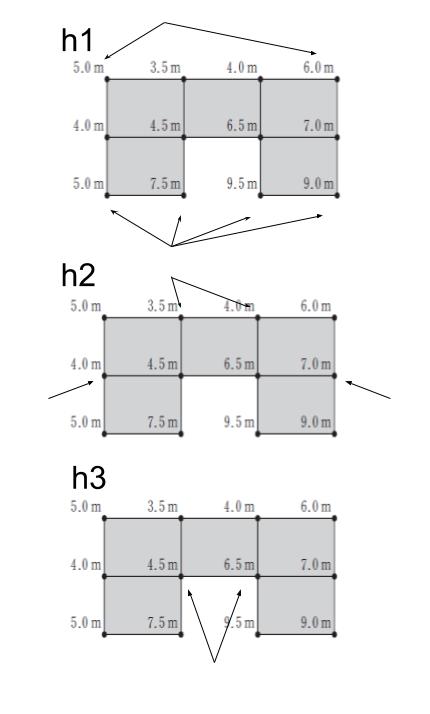
２：下図のようになるので

• Σh₁ = 5.0+6.0+5.0+7.5+9.5+9.0 = 42.0
• Σh₂ = 3.5+4.0+4.0+7.0 = 18.5
• Σh₃ = 4.5+6.5 = 11.0
• Σh₄ = なし。

以上より

H = (1×42.0+2×18.5+3×11.0)/(5×4)
=112/20
=5.6

従って、正解は 1 です。