問 題
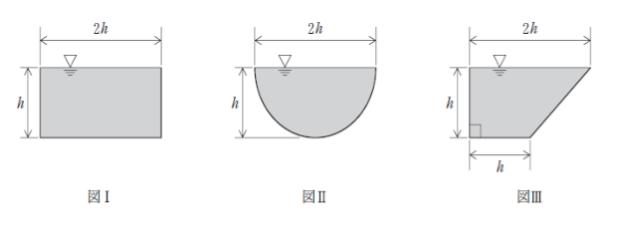
図Ⅰ、Ⅱ、Ⅲに示す断面の開水路に水深hで水が流れているとする。
マニングの式から、図Ⅰ、Ⅱ、Ⅲに示す流れの平均流速を算出した結果をそれぞれV1、V2、V3とするとき、これらの大小関係として最も妥当なのはどれか。
なお、図Ⅰ、Ⅱ、Ⅲの各水路の粗度係数とエネルギー勾配は等しいものとし、図Ⅰに示す断面は長方形、図Ⅱに示す断面は半円、図Ⅲに示す断面は台形とする。
- V1 < V2 < V3
- V1 < V2 = V3
- V1 = V2 = V3
- V1 = V2 > V3
- V1 > V2 > V3
正解 (4)
解 説
マニングの式は絶対に正確に覚えておくべき公式です。
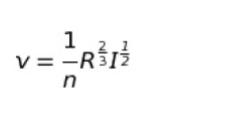
※ R は径深。A/S。Aは流積、Sは潤辺。
粗度係数 n とエネルギー勾配 I が等しいとあるので、A/Sをそれぞれの図について求めます。
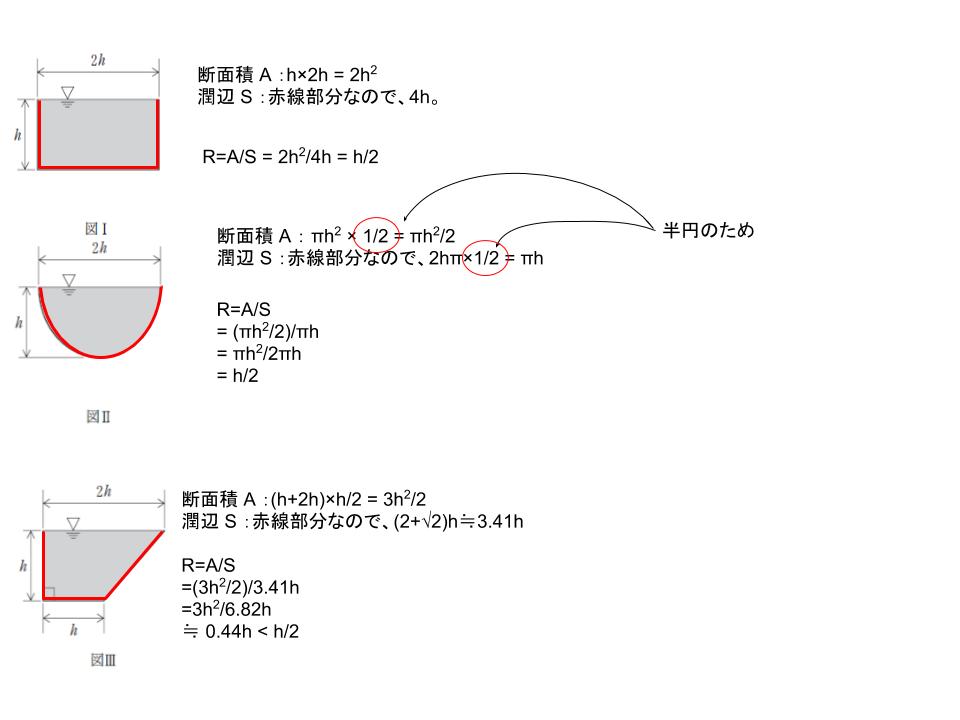
以上より、V1 = V2 > V3 です。
正解は 4 です。

コメント