公務員試験 H26年 国家一般職(電気・電子・情報) No.26解説

　問 題　　　　　

t ≧ 0 で定義された関数 f (t) のラプラス変換を複素数 s を用いて

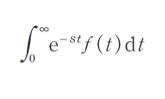
と定義する。

いま、f(t) が次式で表されるとき、そのラプラス変換として最も妥当なのはどれか。
f (t) ＝ e^-3t ＋ 2t  ( t ≧ 0 )、ただし複素数 s の実部は正とする。

 

 

 

 

 

　解 説　　　　　

基本的なラプラス変換である e^-at → 1/(s-a)、 t → 1/s² について覚えていれば、公式からすぐに、1/(s+3) + 2/s² です。

公式を知らなければ、定義に基づいて計算をすれば OK です。※計算が複雑で、非推奨です。基本的なラプラス変換は公式を覚えておくべきと考えられます。

e^-st f(t) = e^-st(e^-3t + 2t) = e^-(s+3)t + 2t e^-st です。各項を積分してみます。
∫ e^-(s+3)t dt = e^-(s+3)t/-(s +3) となります。

また
∫ t e^-st
= ∫ t (e^-st/-s)’
= te^-st/-s -∫  (e^-st/-s)
= te^-st/-s – e^-st/s² です。

どの積分結果の項も t = ∞ の時には 0 になるため、定積分の結果は t = 0 を代入したもの※ただし符号は逆　です。よって、確かに 1/(s+3) + 1/s² です。 2t の部分を 2 倍すれば、1/(s+3) + 2/s² です。

以上より、正解は 1 です。