問 題

図のように真空中に間隔 d 、幅 l の平行平板電極がありこれに電圧 V が印加され、電極間に一様な電界が生じている。電気量-e 質量 m の電子を速さ v で電極と平行に入射させたところ,電子は電極間を通過して飛び出した。電子が電極間へ入射する方向と電子が電極間から飛び出す方向とのなす角を θ とするとき tanθ として最も妥当なのはどれか。
ただし電界は電極間にのみ存在するものとし入射した電子は電極には衝突しないものとする。また紙面に垂直な方向の成分及び重力の影響は考えないものとする。なお電極間を飛び出した後の電子の速度の電極と平行な成分を vx、 電極に垂直な成分を vy とすると tanθ = vy/vx と表される。
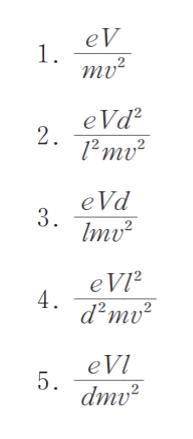
解 説
まず、特殊な具体例を考えることで正解をしぼります。 l = 0 なら電極がないため、荷電粒子は直進するだけです。つまり、vy = 0 で、tan θ = 0 のはずです。よって「分子」に l が含まれるはずだから、正解は 4 or 5 です。
次に「一様な電界」とあるので、V = Ed、その中にある荷電粒子が受ける力は F = qE です。これは基礎知識です。Fy = e(V/d) と表すことができます。荷電粒子の質量は m なので、受ける力と質量がわかったから、この粒子の加速度が F = ma よりわかります。 a = eV/dm・・・(1) です。
vy = at なので、t がわかればよいです。本問における t は「電極間を通過するのにかかる時間」です。道のりは l です。速度は v です。l = vt なので、t = l/v・・・(2) と表すことができます。
(1),(2)より、vy = at = (eV/dm)×(l/v)・・・(3) です。
vx = v ・・・(4)です。
(3)、(4)より
tan θ = vy/vx は、以下のように計算できます。

以上より、正解は 5 です。

コメント