公務員試験 H25年 国家専門職(教養) No.19解説

　問 題　　　　　

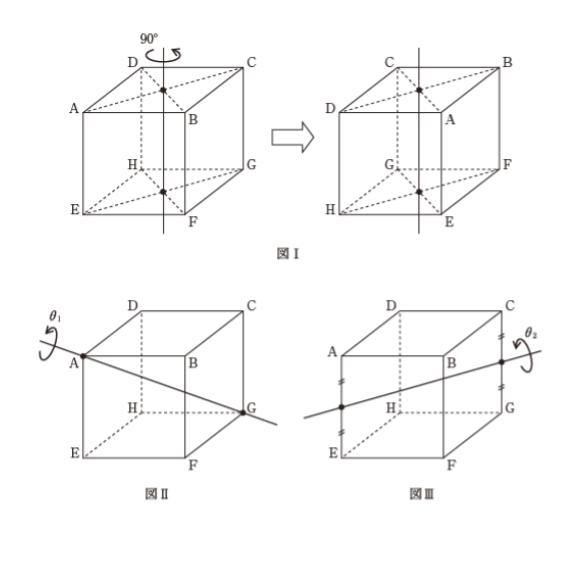
図Ⅰのように、立方体は、向き合う二つの面におけるそれぞれの対角線の交点を通る直線を回転軸として90°回転させると元の状態と見比べて見分けがつかない状態になる。

図Ⅱのように、立方体の頂点Ａ、Ｇを通る直線を回転軸としたときに、元の状態と見比べて見分けがつかない状態になる最小の回転角 θ₁（＞0）及び、図Ⅲのように、辺 AE、CG それぞれの中点を通る直線を回転軸としたときに、元の状態と見比べて見分けがつかない状態になる最小の回転角θ₂（＞ 0）の組合せとして最も妥当なのはどれか。

•  θ1  　　θ2

1. 90° 　　120°
2. 90° 　　180°
3. 120°　   90°
4. 120° 　  180°
5. 180°　   90°

 

 

 

 

 

　解 説　　　　　

図Ⅰにおける点A,B,C,Dのように、『回転軸と面の交点から見て最短かつ等距離にある点』に注目し、それらの点が入れ替わる角度に注目すればよいと考えられます。図Ⅰであれば、最短等距離にある点が４つあるので、360 ÷ 4 = 90°です。

図Ⅱでは、点Aと等距離にあるのがB,D,Eと３点なので、360 ÷ 3 = 120°　と考えられます。

図Ⅲでは、回転軸と面の交点から見て等距離にあるのがAとEだけなので、 360 ÷ 2 = 180 と考えられます。

以上より、正解は 4 です。