公務員試験 H25年 国家一般職(化学) No.2解説

　問 題　　　　　

図のように、線分 AB と AC がそれぞれ点 P,Q で円に接している。円周上の点 R が図に表す位置にあるとき、線分 AB と AC のなす角 θ はいくらか。

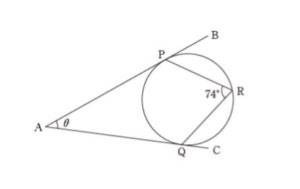
1. 26°
2. 28°
3. 30°
4. 32°
5. 34°

 

 

 

 

 

　解 説　　　　　

円が出てきたら、中心と特徴的な点を結んでみるとヒントが見つかることが多いです。

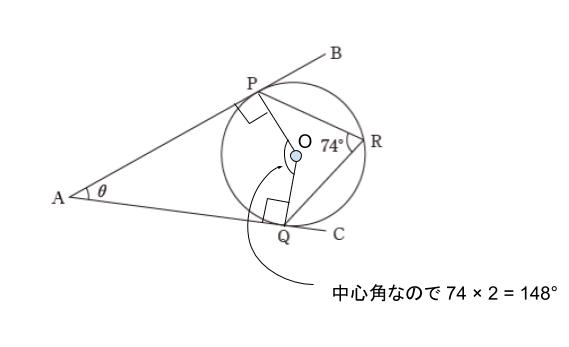
上図のように、四角形 APOQ に注目すれば、APO、AQO が直角で、POQ は中心角なので 148°です。従って、残りの一つの角度である PAQ は、内角の和が 360°にならなければならないため 32° とわかります。

以上より、正解は 4 です。