問 題
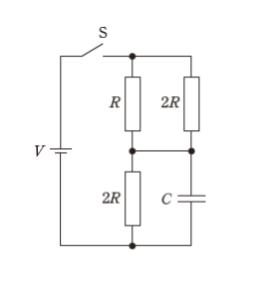
図のような、起電力 V の直流電源、抵抗値が R 及び 2R の抵抗、静電容量が C のコンデンサ、スイッチ S からなる回路がある。この回路のスイッチ S を閉じて十分に時間が経過したとき、コンデンサに蓄えられている電気量として最も妥当なのはどれか。
- 2/5 CV
- 3/4 CV
- 4/5 CV
- 5/4 CV
- 3/2 CV
正解 (2)
解 説
十分に時間が経つと、コンデンサの両端に+、-の電荷が蓄えられます。この時、コンデンサの極板間には電流が全く流れていないため「抵抗が無限大とみなす」のがポイントです。電流回路としては、コンデンサを無視します。下図のような回路として考えるということです。
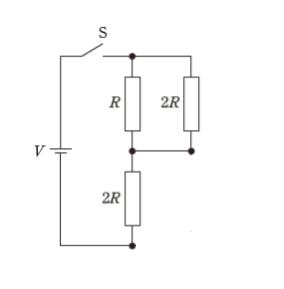
そうすると、抵抗 R と2R の並列部分と、抵抗2R の部分がつながった回路とみなすことができます。
合成抵抗を計算すると、並列の部分(Rと2R)は
R×2R/R+2R
= 2R2/3R
= 2R/3 です。
2R/3 と 2R の直列なので、合成するために足すと (8/3)R です。全体の電圧が V なので、流れる電流は 3V/8R です。
コンデンサ部分の電気量を知るためには、コンデンサの基本式 Q = CV から V がわかればよいです。コンデンサの部分と並列の位置にある2Rの抵抗に注目します。※並列であれば、電圧が同じだからです。
V = RI なので、RI を計算すると、2R × 3V/8R = 3V/4 です。Q=CV なので、3/4 CV が答えです。
以上より、正解は 2 です。

コメント