公務員試験 H25年 国家一般職(土木) No.25解説

　問 題　　　　　

図のように断面積 A のタンクの底面に長さ h 、断面積 a の円管をつけてタンク内にたまった水を排出していく。

タンクの水深が H になった瞬間に円管から排出する水の流量 Q として最も妥当なのはどれか。

ただし、重力加速度の大きさを g とし、エネルギー損失は無視できるものとする。

 

 

 

 

 

　解 説　　　　　

ベンチュリー管と見て、公式より、正解は 1 です。

ベルヌーイの定理を用いても解けます。

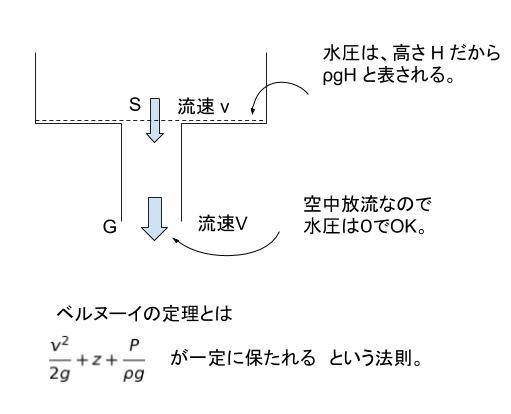
S点とG点について（Start,Goal を意識しています。）円管入り口であるS点を高さの基準と見てベルヌーイの法則を考えれば

v²/2g + 0 + ρgH/ρg = V²/2g – h ・・・（１）です。

※B点において、空中に放流しているため、水圧は 0 です。

両辺に 2g をかけて、整理すると

v² + 2gH = V² -2gh ・・・（１）’

また、連続の式より

Q = Av = aV ・・・（２）が成り立ちます。

これを変形して v = a/A V として（１）’ に代入します。

代入してがんばって式変形していき、V² = ・・・とした上で求めるのがQ = 「aV」 だったので、a² をかけた所までが以下になります。

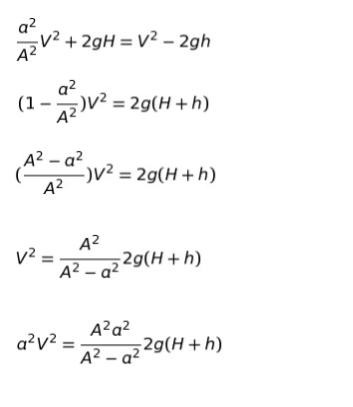
最後の式の辺辺 √ とれば左辺がaV,つまりQ です。そして、右辺が答えです。

よって、確かに選択肢 1 の形になっています。