問 題
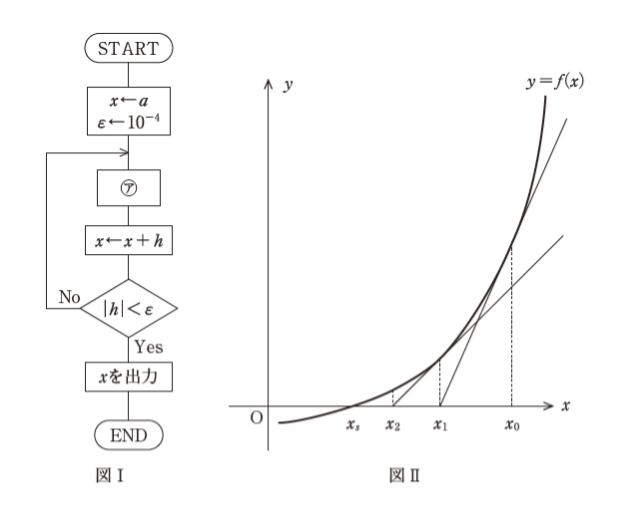
図Ⅰは、正の実数 a の正の平方根 √a の近似値を、方程式 x2 = a の解として、ニュートン法によって求めるためのフローチャートである。近似解の修正値 h の絶対値が ε 未満になったときに、その近似解を出力して停止する。図Ⅰ中の㋐に当てはまるものとして最も妥当なのはどれか。
なお、ニュートン法は、図Ⅱのように、適当な初期値 x0 から x1 、x2 、… を繰り返し計算することによって、方程式 f (x) = 0 の解 xs の近似値を求める方法である。k + 1 番目の近似値 xk+ 1 は、k 番目の近似値 xk から、y = f (x) の点 ( xk、f (xk) ) における接線と x 軸との交点 ( xk+ 1、0 ) の x 座標として求められる。
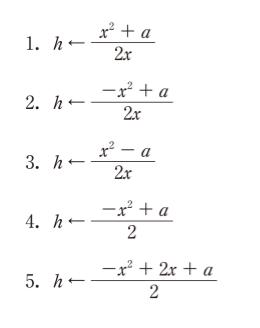
正解 (2)
解 説
x2 = a を、右辺を 0 にすると x2 – a = 0 です。問題文の図は y = x2 – a のグラフと考えられます。すると、初期値 x0 において、点の座標は (x0、x02 – a) です。この点における接線の傾きは、y’ = 2x より、2x0 です。接線の式は y = 2x0 x – x02 – a と表すことができます。
接線の式において y = 0 を代入して x について解けば、x = (x02 + a)/2x0 です。 x0 + h = (x02 + a)/2x0 を解くと h = (- x02 + a)/2x0 となります。
以上より、正解は 2 です。

コメント