問 題
ある市において犬や猫を飼育している世帯数を調査したところ次の結果が得られた。
○ 犬か猫だけ又はその両方を飼育している世帯数は3,800世帯である。
○ 犬を飼育している世帯の 1/7 は猫も飼育している。
○ 猫を飼育している世帯の 9/41 は犬も飼育している。
このとき猫だけを飼育している世帯数として正しいのはどれか。
- 1,260世帯
- 1,280世帯
- 1,300世帯
- 1,320世帯
- 1,340世帯
解 説
まず初めに以下のようなベン図(2成分)を考えると、式を立てやすいのではないでしょうか。
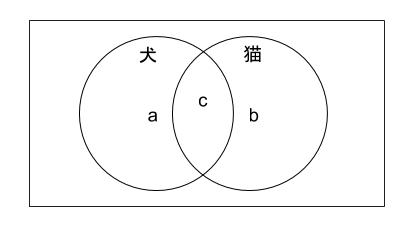
犬のみ飼育している世帯数を a、猫のみを飼育している世帯を b、両方飼育している世帯を c とすると
a+b+c = 3800
(a+c)/7 = c
9(b+c)/41 = c
と条件をまとめることができます。
「(a+c)/7 = c」の両辺を 7 倍して、同類項まとめると、「a = 6c」 となります。同様に「9(b+c)/41 = c」 の両辺を 41倍することで、「9b = 32c」 です。
求めるのは b です。以下、解法を2つ示します。どちらでもできるようにしておくとよいと思います。
【解法1:他の文字を全部 b で表す】
9b = 32c なので、「c = 9b/32」 です。a = 6c の c に 9b/32 を代入すれば、「a = 54b/32」 です。a + b + c = 3800 なので、54b/32 + b + 9b/32 = 3800 ということになります。
95b/32 = 3800 → 両辺に 32/95 をかければ b = 1280 です。正解は 2 です。
【解法2:比を出す(連比)】
a = 6c より、a:c = 6:1です。同様に 9b = 32c より、b:c = 32:9 です。a:c = 6:1 → 54:9 とすれば、a:b:c = 54:32:9 とわかります。
あわせて 3800 世帯なので、比で言う 95 が 3800世帯です。よって、比で言う 1 が 40 世帯です。求めるのは b なので、b = 40 × 32 = 1280 世帯です。
正解は 2 です。

コメント