問 題
A~Dの4チームでラグビーの総当たり戦を行い次のルールで順位を決めることとした。
順位の決め方
獲得ポイント総数(勝敗ポイント総数と加点ポイント総数の合計)で順位を決める。獲得ポイント総数の多い方が順位が高い。ただし獲得ポイント総数が同じ場合は同順位とする。
1試合の結果で与えられるポイント
勝敗ポイント
- 勝ち:4ポイント
- 引き分け:2ポイント
- 負け:0ポイント
加点ポイント
- 試合の勝敗にかかわらず1試合で四つ以上「トライ」を取った場合:1ポイント
- 7点差以内の得点で負けた場合:1ポイント
全試合終了後の各チームのトライ総数加点ポイント総数引き分け試合数は次のとおりである。この場合確実にいえるのは次のうちどれか。なお「トライ」は得点手段の一つである。
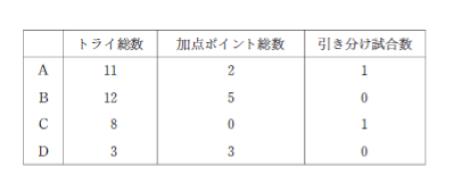
- Aの獲得ポイント総数は8ポイントである。
- AとCの勝ち数は同じである。
- Bの勝ち数は負け数より多い。
- CはDに8点以上の差で負けている。
- Dの順位は3位である。
解 説
まず、引き分け試合数から見て「AーC」は引き分けです。次に、Dのトライ総数が 3 にもかかわらず、加点ポイント総数が 3 である点に注目します。すると、Dが試合した3試合は全て7点差以内で負けたとわかります。
ここまでで、選択肢 4,5 は誤りとわかります。
選択肢 4 ですが、C-Dは、Dの負けですが、7点差以内のはずです。
選択肢 5 ですが、Dは全敗なので、A、B、Cが最低でも勝敗ポイントで4ポイント以上となります。そしてDは合計ポイントが3ポイントなので、最下位です。
次に、加点ポイントがやけに多い B に注目すると、トライ4個ずつ取ったとすれば加点ポイントは3試合で3です。後2ポイントは、負けて7点差だったということになります。BはDには勝っているため、BはA,Cに7点差以内で負けているとわかります。
選択肢 1 ですが、AはB,Dに勝利し、Cとは引き分けです。加点ポイントと加えて、合計ポイントは 12 ポイントです。8ポイントではありません。
選択肢 2 は、正しい記述です。CはB,D に勝利し、Aとは引き分けなので、AとCは共に勝ち数2です。
選択肢 3 ですが、B は1勝2敗です。よって誤りです。
以上より、正解は 2 です。

コメント