問 題
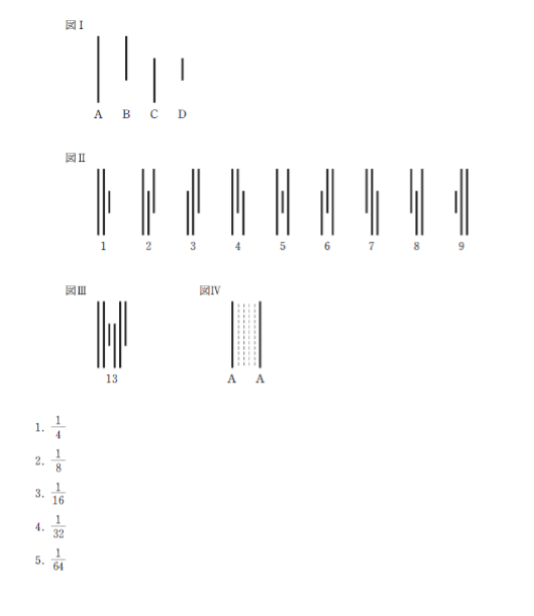
図Ⅰにあるような4種類のバーA~Dがある。これらのうちから3本を図Ⅱのように組み合わせて「1」~「9」の数字を示すこととする。2桁以上の数を示す場合はこれらのバーを横に並べる。例えば「13」を示す場合は図Ⅲのようになる。
いま図のとおり両端にAのバーを置きその間の4本分のスペースにA~Dを無作為に並べる場合並んだ6本のバーが2桁の奇数を示す確率はいくらか。なお同じ種類のバーは何本用いてもよいものとする。
解 説
図Ⅳにおける、両端の A の間にバーが入るスペースを、左から以下のように①、②、③、④と名前をつけます。

【左側の数値を表す 「A①②」 に関して】
①、②に、図ⅠのA~Dのどれかのバーがそれぞれ入ります。4通り×4通りで 16 通り考えられます。
図Ⅱを見ながらゆっくり考えると、「A①②」 が表す数値として考えられるのは、1,2、4、5 のどれかです。つまり AAD か、ACBか、ABCか、ADA というバーの組み合わせです。これ以外のバーの組み合わせでは、図Ⅱにないため、数値を表しません。
従って、①、②に許される組み合わせは「AD、CB、BC、DA」のみです。16通りのうち4通りなので、4/16 = 1/4 です。
【右側の数値を表す 「③④A」 に関して】
2桁の奇数でなくてはならない、という点に注意します。
やはり図Ⅱを見ながらゆっくり考えると、「③④A」 が表す数値として考えられるのは、5,6,8,9のどれかです。そして、奇数であれば右側の数値は1,3,5,7,9のどれかでなければなりません。よって、5or 9でなければいけません。
つまり、③、④に許される組み合わせは「AD」or「DA」のみです。16通りのうち2通りなので、2/16 = 1/8 です。
以上より、1/4 × 1/8 = 1/32 が求める確率です。正解は 4 です。

コメント