問 題
A~Eの5人が卓球でダブルスの試合を次の対戦表に従って行い個人ごとに順位をつけることにした。各人が加わった組の勝ち・負けをそれぞれその者の勝ち・負けとして各人の勝敗数をカウントし勝利数の多い順に上位から順位を決める。
ただし引き分けはないものとする。なお勝利数が同じ者がいた場合には同順位とし次の順位は同順位とした人数分だけ繰り下がるものとする。
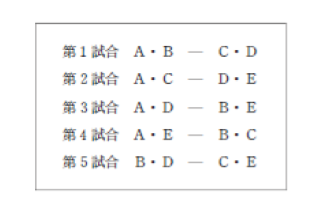
第1試合を行ったところA・B組が勝ったのでAとBはそれぞれ1勝0敗となりCとDはそれぞれ0勝1敗となった。すべての試合が終わった時点で次のことが分かっているとき確実にいえるのはどれか。
○ 1位になった者はAとEの2人だった。
○ Bは2勝2敗だった。
- Bは3位Cは5位であった。
- CとDの2人は3位であった。
- A・C組はD・E組に勝った。
- A・D組はB・E組に勝った。
- Eが加わった組はCが加わった組に対して2勝した。
解 説
1つの試合で1勝すると、2人に1勝ずつカウントされる、というルールなので、5試合で計10勝が割り振られます。 B が 2勝で、1位の A,E がいることから A,Eは最低 3 勝ずつしています。さらに、AとEが対戦をすることがあるので、共に4勝(全勝)はありえません。以上より、 A,E が3勝1敗とわかります。
第4試合のA,E組がもしも負けていたら、A,Eが対戦する第2試合や第3試合で、どうやってもAかEがさらに1敗してしまい「A,Eが共に3勝1敗」にすることができなくなります。従って、第4試合はA・E組の勝利とわかります。
第5試合で E を含む C・E組がもし負けていると、第2、第3試合で E を含むグループは1敗もできなくなります。しかし、そうすると A が2敗になるため矛盾です。従って、第5試合は C・E組の勝利とわかります。
ここまでの考察から、Bが1勝2敗分まで確定となります。 B は2勝2敗なので、第3試合で B を含むグループである B・E組が勝利です。これにより、Eを3勝1敗に仕上げるために、第2試合は A・C組が勝利とわかり、全試合の勝敗が、以下のように確定します。
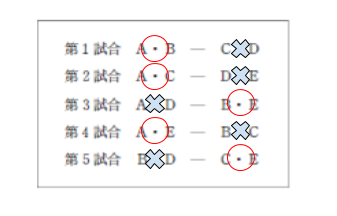
結果、A 3勝1敗、B2勝2敗、C2勝2敗、D0勝4敗、E3勝1敗です。順位は1位が A,E,3位が B,C 5位が D です。
従って、正解は 3 です。

コメント