公務員試験 H24年 国家一般職(土木) No.30解説

　問 題　　　　　

図のような粘着力を有しない砂の三軸圧縮試験（CD条件）において、側圧 σ₃ = 100kN/m² を一定に保ったまま軸応力を増加したところ、σ₁ = 300kN/m₂ で破壊した。

このときの土の強度定数である内部摩擦角Φ_d 及び水平面からのすべり面の角度θ_f の組合せとして最も妥当なのはどれか。

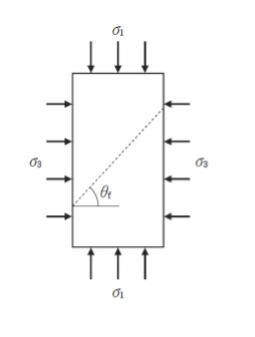
• 内部摩擦角Φ_d 　すべり面角度θ_f

1. 　　30° 　　　　　　30°
2. 　　30° 　　　　　　60°
3. 　　45° 　　　　　　45°
4. 　　60° 　　　　　　30°
5. 　　60° 　　　　　　60°

 

 

 

 

 

　解 説　　　　　

(σ₁+σ₃)/2 = 200、(σ₁ – σ₃)/2 = 100 なので、中心が(200,0), 半径が 100であるような円をかきます。

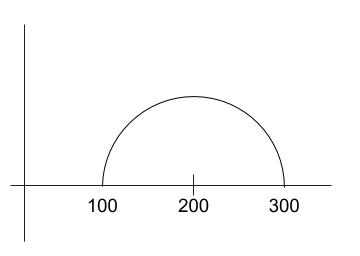
この円上の点の座標は、ある破壊面（本問の破壊面はθ_f をなしている点線）についての垂直応力と、せん断応力を表します。x 座標が垂直応力、y座標がせん断応力です。

すなわち、以下のようになります。

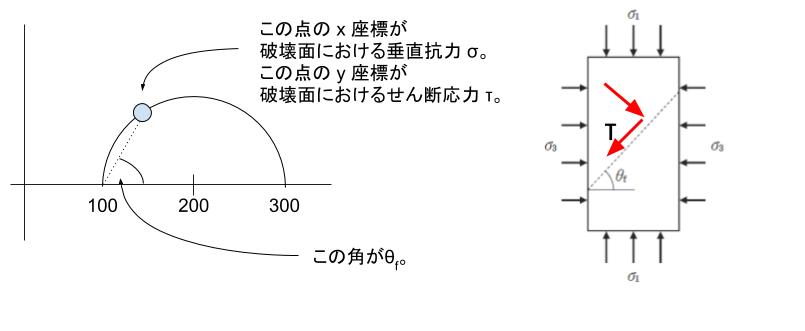
モールの応力円において、ちょうど破壊面となる θ_f における円上の点に対する接線は「クーロンの破壊線」です。

この直線の式は普通の1次関数のようにy = ax + b ではなく、s = c + σtanΦ　と書くことが通例です。s は結局の所 τ と同じですが「せん断強さ」　と呼ばれます。c は「粘着力」です。Φ が「内部摩擦角」です。

本問では「粘着力は有しない」とあるので、s = σtanΦ　です。つまり、原点を通る直線となります。従って、以下の図のようになります。

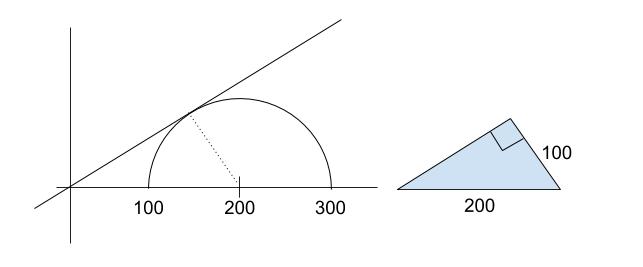
辺の比が 1：２なので特殊な直角三角形で、残りの角度は 30°、60°とわかります。従って、Φ = 30 °です。

正解は 1 or 2 となります。

θ_f ですが、補助線を引くと正三角形となり、 60°です。

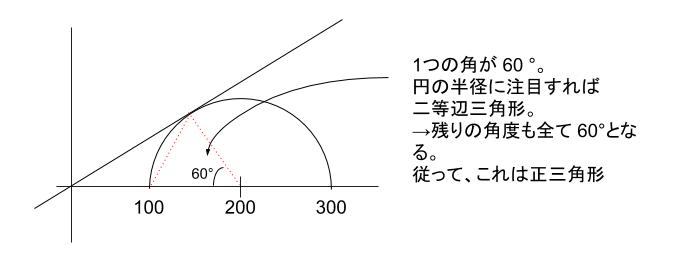
ちなみに正確な角度を求めなくても選択肢から候補は 30°か 60°ですが、図より明らかに 30°よりは大きいと判断できます。

以上より、正解は 2 です。