公務員試験 H24年 国家一般職(土木) No.4解説

　問 題　　　　　

曲線 y = x² – 2x と x 軸で囲まれた図形をx 軸のまわりに一回転させてできる立体の体積はいくらか。

1. 16/15 π
2. 4/3 π
3. 8/5 π
4. 32/15 π
5. 38/15 π

 

 

 

 

 

　解 説　　　　　

y = x² – 2x のグラフは、以下のようになります。

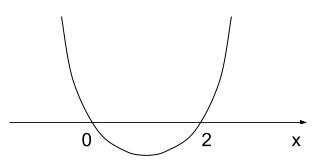
解法 1 【積分】
x 軸周りの回転なので、「π y²を積分」します。囲まれた部分を回転なので
π ×（「上端を表す式」ー「下端を表す式」）²　を積分して計算します。以下のようになります。

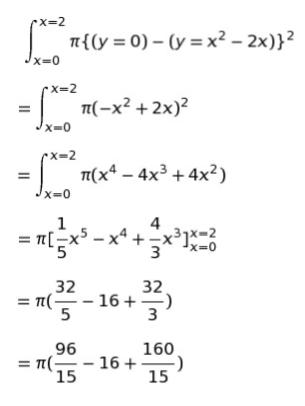
以上より、体積は 16/15 πです。
よって、正解は 1 です。

解法２【大雑把な評価】
積分がきらいな人は『面積の大雑把な評価』で選択肢をしぼる　という手法をぜひ身につけておくとよいです。１つでも選択肢を切れないか考えます。面積の大雑把な評価のために求める立体に似た、簡単な図形として半径 1 の球を考えて比較します。以下の図のようなイメージです。

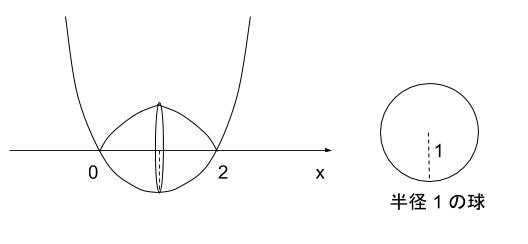
求める立体の体積は半径 1 の球よりも少し小さいと判断できます。半径 1 の球の体積は 4/3 π　です。（球の体積の公式は基本知識です。）選択肢 の数字は選択肢 1 からだんだん大きくなっており、選択肢 2 が 4/3 πです。従って、答えは 4/3 πよりも小さい 16/15 πと考えられます。

以上より、正解は 1 です。