公務員試験 H24年 国家一般職(土木) No.1解説

　問 題　　　　　

sin²θ = cosθ である時

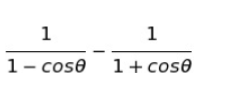
の値はいくらか。

1. 1
2. √5 －1
3. 2
4. √5
5. √5 ＋ 1

 

 

 

 

 

　解 説　　　　　

まず「分母が違う分数の引き算」（1/2  ー 1/3 のようなもの ）であれば分母を通分するので、本問でも分母を通分してみます。

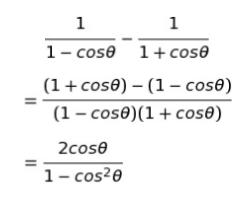
となります。ここで「三角関数の基本公式」である
sin²θ + cos²θ = 1 を用いることで、分母の１－cos²θは 「sin²θ」 と書き換えることができます。

本問では sin²θ = cosθ なのでさらに書き換えると、2cosθ/cosθ　です。従って、約分できて、値が 2 とわかります。

以上より、正解は 「3」 です。