問 題
論理式![]() と等価なものは、次のうちではどれか。ただし
と等価なものは、次のうちではどれか。ただし![]() は論理変数 P の否定を、「+」は論理和を、「・」は論理積を表すものとする。
は論理変数 P の否定を、「+」は論理和を、「・」は論理積を表すものとする。

正解 (2)
解 説
Aとして 0 or 1、B として 0 or 1 のそれぞれのパターンで、各部分がどうなるかを表にまとめます。論理式を分解して評価していきます。以下、否定については「Aバー」のように表記します。
「Aバー ・ B」 は、AバーとB の論理積、つまり AND をとる、ということです。「Aバーと B が共に 1」 の時だけ 「1 を出力」します。従って、A 0、B 1 の時だけ 1 出力です。真理値表でまとめると以下のようになります。

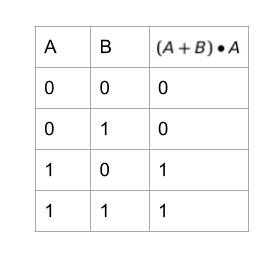
(A+B)・A は、A = 1 であれば、出力が 1 です。
与えられた論理式は
「Aバー ・ B」と「(A+B)・A」という2つの部分の 「論理和」、つまり OR をとるという論理式です。従って「A = 0、B = 0 のときだけ 0、のこりは 1」 です。これをふまえ、選択肢を検討します。
すると、選択肢 2 の 「A + B」 が、まさに「A = 0、B = 0 のときだけ 0、のこりは 1」 です。
以上より、正解は 2 です。

コメント