問 題
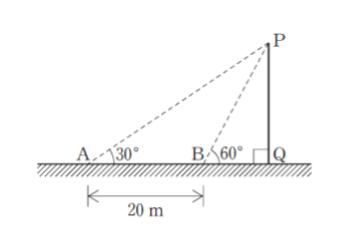
図のように地点 A から柱 PQ の先端 P の仰角を測ると 30°であった。次に柱に向かって水平に 20m 進んだ地点 B から P の仰角を測ると 60°であった。このときの柱 PQ の高さはいくらか。

正解 (4)
解 説
公務員試験頻出の「90°,60°,30°」の直角三角形がポイントです。辺の比が 1:2:√3 になります。
選択肢 1 が仮に正解だとすると
PQ = 8√2cm です。⊿PQB に注目すれば、BQ の長さが 8√2/√3 となります。⊿PQA に注目すれば PQ × √3 = 8√6 = AQ のはずです。しかし AQ = AB + BQ = 20+8√2/√3 となります。8√6 と20+8√2/√3は、明らかに異なります。よって、選択肢 1 は誤りです。
以下、選択肢を代入していくと、AQ = 10√3 の時 BQ = 10。AQ = AB + BQ = 20 + 10 = 30。AQ × √3 = 30 となり、うまくいきます。
別解
BQ = x とおくと、PQ = √3x です。PQ × √3 = 3x = AQ です。そして、AQ = AB + BQ = 20 + x です。よって 20 + x = 3x ∴x = 10 →PQ = 10√3 とわかります。
以上より、正解は 4 です。

コメント