問 題
図のような,面積が36 の正六角形A,Bについて,それぞれの網掛け部分の面積の組合せとして最も妥当なのはどれか。
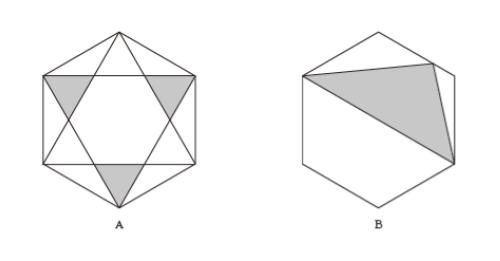
A B
1. 4 10
2. 4 12
3. 4 15
4. 6 10
5. 6 12
正解 (5)
解 説
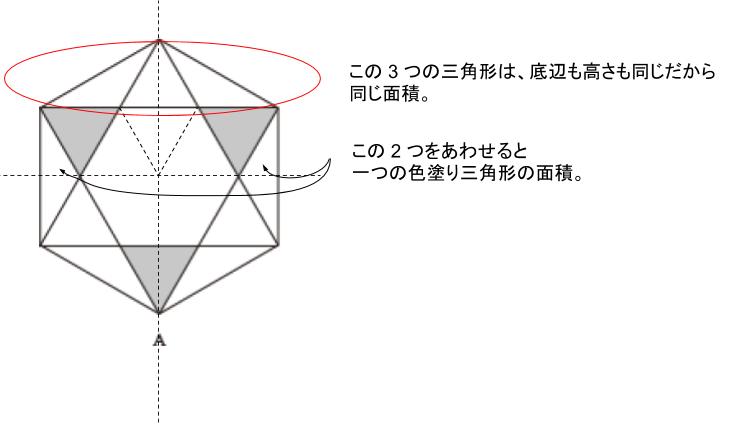
A について、以下のように補助線を引くことで、色塗り三角形と同じ面積がいっぱいできます。そして、六角形の上半分が色塗り三角形 9 個分とわかります。(赤丸で囲った部分が、色塗り三角形 3 つ分。)
面積 36 の半分が 18 です。上半分が、色塗り三角形 9 個分で 面積 18 だから、一個の色塗り三角形の面積が 2 とわかります。よって、A の面積は 2 × 3 = 6 です。
次に B ですが、これはまず等積変形をします。正六角形の一辺と、色付き三角形の底辺が平行である点がポイントです。(下図左側の↘二本が 平行)
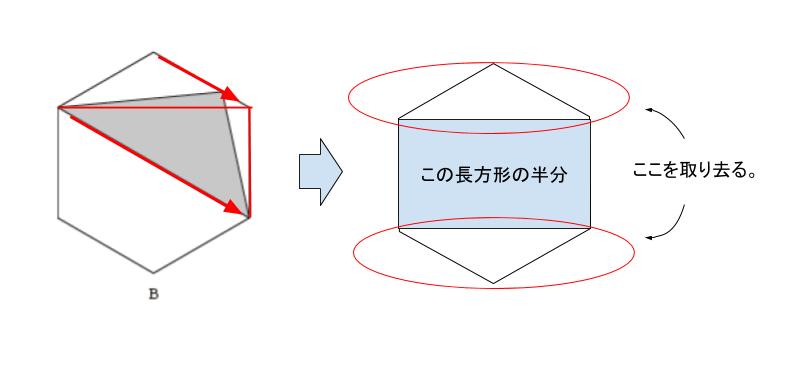
するとこれは、正六角形から、さきほどの図における赤丸で囲った部分(面積6)を2個分取り去って残る、長方形の半分の面積とわかります。従って B の面積は (36ー6×2)/2 = 12 です。
以上より、正解は 5 です。

コメント