問 題
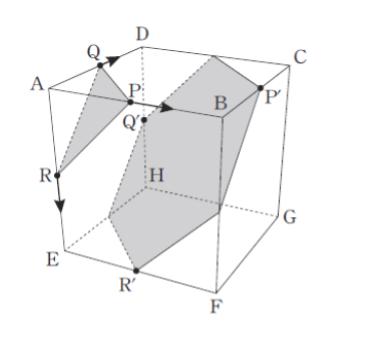
図のように一辺の長さが1の立方体 ABCDEFGH とその辺の上を動く点P Q Rを考える。
今3点P Q Rは時刻0において、頂点Aを同時に出発しいずれも毎秒1の速さで、PはA→B→C→G、QはA→D→H→G 、RはA→E→F→Gの経路で移動して,3秒後に頂点Gで停止するとする。(P′ Q′ R′はそれぞれP Q Rが頂点Aを出発してから1.5秒後における位置を示している。)
時刻 x において3点P Q Rを通る平面でこの立方体を切断したときの断面積をS (x) とおくとき y = S (x) のグラフを表しているものとして最も妥当なのはどれか。
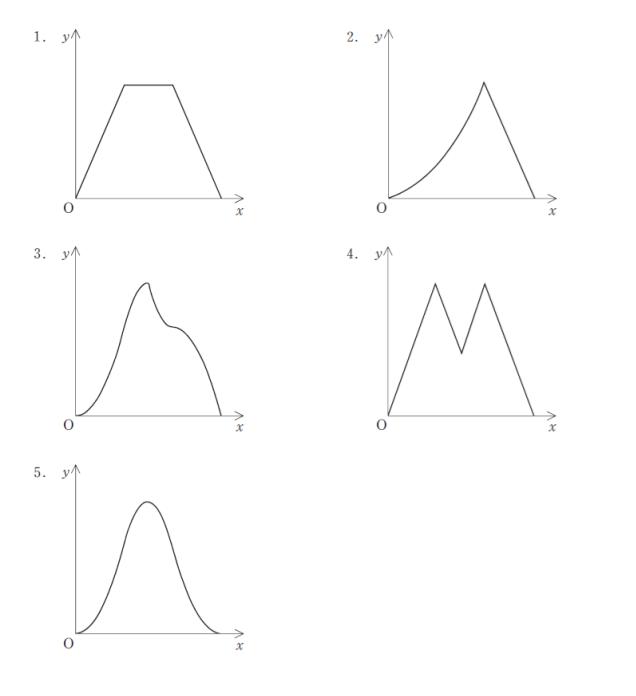
正解 (5)
解 説
まず、0~1 秒後までを具体的に考えると、三角形が どんどん大きくなっていきます。例えば、0.1 秒後と、0.2 秒後 を考えれば、「底辺 も 高さ も2倍になる」と考えられます。この時、面積は「時間の2乗に比例する」とわかります。であれば、グラフの出だしは「曲線」になるはずです。従って、選択肢 1,4 は誤りです。
さらに、2~3 秒後までを具体的に考えれば、これは 0~1 秒後の真逆 です。であれば、グラフの出だしと終わりは、対称的でなければなりません。よって、選択肢 2,3 は誤りです。以上より、正解は 5 です。

コメント