公務員試験 H26年 国家一般職(化学) No.22解説

　問 題　　　　　

ケイ酸四面体シートの Si の含有量に関する次の記述のア イ に当てはまるものの組合せとして最も妥当なのはどれか。ただし Si の原子量を28、アボガドロ数を6.0× 10²³、 √2 = 1.4、√ 3 = 1.7とする。

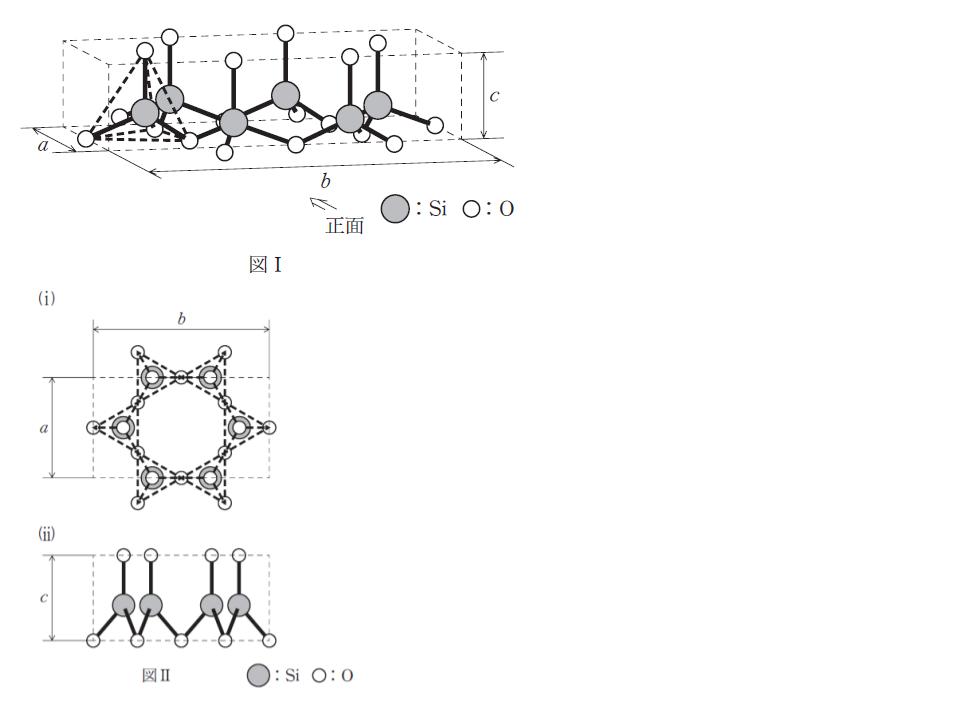
「Si 原子は、四つの O 原子に囲まれた正四面体を形成する。ケイ酸四面体シートは SiO₄ の正四面体が O 原子を共有し図Ⅰに示す点線で囲まれた直方体 ( 各辺を a、b、 cとしその長さをそれぞれ a , b , c とする。) を基本単位として、辺 a 辺 b の方向に繰り返し広がりシートを形成したものである。

ここでこの直方体の基本単位を上及び正面から見ると図 Ⅱ の (ⅰ)  及び (ⅱ) となる。a，ｂ，ｃ には a : b : c = ア の関係があり、a を0.52nm とすると直方体の基本単位の単位体積当たりのSiの質量はイ g/cm³ となる。」

 

 

 

 

 

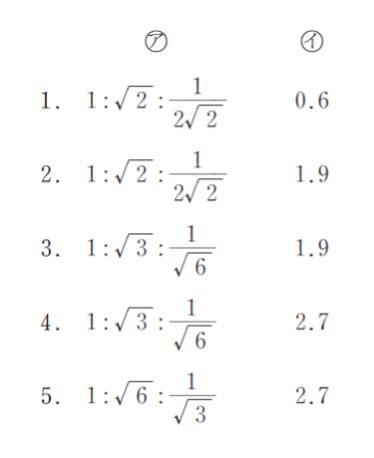
　解 説　　　　　

図Ⅱの (i) が読めるか　というのが、ア で聞かれていることになります。以下のように注目することで、正三角形の一辺を x とおくと、まず直方体の 「a」 は 2x とわかります。

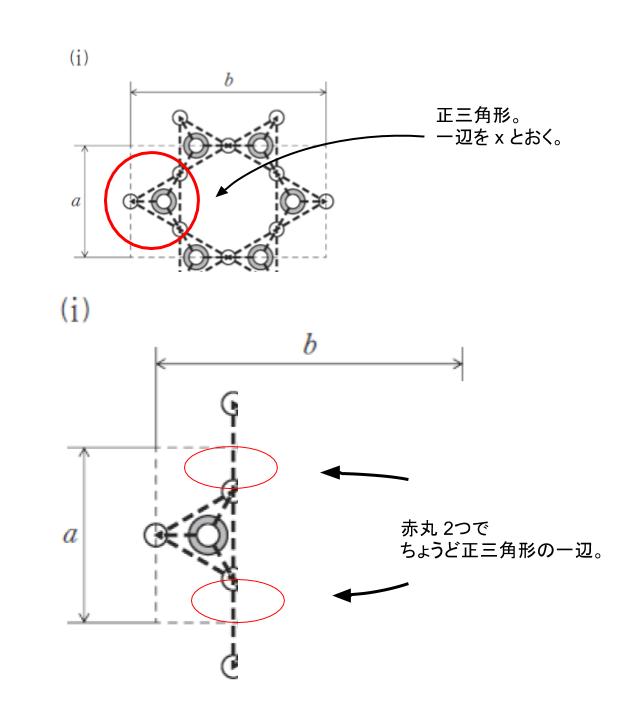
次に、直方体の 「b」 は、以下のように注目することで 2√3 x と表すことができます。

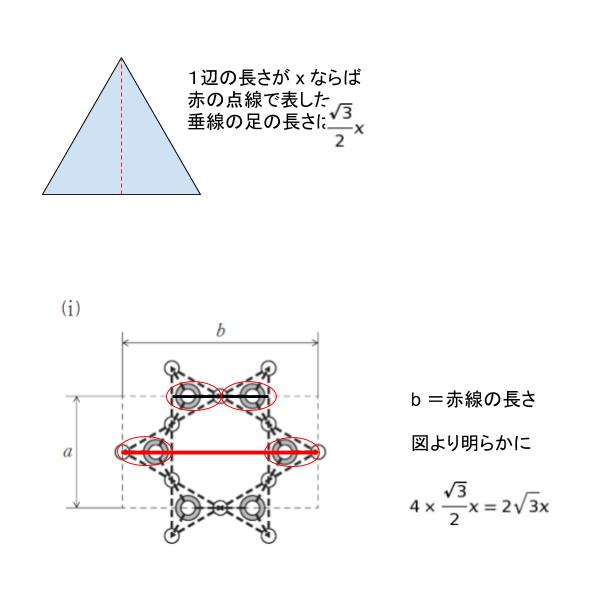
従って、a : b = 2x : 2√3x = 1:√3 です。正解は 3or 4 です。選択肢より、a : b : c は 1：√3：1/√6 とわかります。

次に、単位体積当たりの Si の質量を考えます。ア のおかげで直方体の各辺の長さは a を用いて、b = √3a、c = a/√6 と表すことができます。従って、V = abc = a³/√2 です。選択肢を見るとそこまで厳密な解は必要ないので a を 0.5nm と近似します。n = 10^-9 です。V = (0.5×10^-9)³/√2 m³です。

ここで イ の単位が、g/cm³ であることに注意します。1m³ とは１ｍ四方で、1m = 100cm なので

1m³
= 100×100×100 cm³
= 10⁶ cm³ です。

従って
V = (0.53 × 10^-27/√2)  × 10⁶ cm³
∴ V = 0.53/√2 ×10^-21 cm³ ・・・（１）です。

一方、図Ⅰ、Ⅱより（特に図Ⅱ(i) より）基本単位の中に Si は４個入っていると考えられます。1mol = 6.0×10²³個で 28g なので、1個だと 28÷(6.0×10²³) g です。書き換えると 28/6 × 10^-23 g です。

4 個だと 4×(28÷6.0) ×10^-23)g
=112/6.0 ×10^-23 g
=1.12/6.0 × 10² × 10^-23
=1.12/6.0 × 10^-21 g ・・・（２）となります。

求めたいのは（２）÷（１）です。10^-21 がうまく打ち消し合ってくれるので結局
「1.12/6 ÷ 0.5³/√2 」を評価すれば OK です。0.5 = 1/2 なので0.5³ = 1/8 です。√2 =  1.4 なので、割る数は 1/1.4 × 8 =1/11.2 です。

従って
1.12/6 ÷ 1/11.2
=1.12/6 ×11.2/1
= （(1.12)² × 10）/6 と表せます。
 
分子の方が、12 付近の値 なので「12/6 = ２」に近い数値を選べば良さそうと評価できます。選択肢から選ぶなら 1.9 です。※ a を少し小さめ（0.52→0.5）に評価しているため V が小さめだから、わる数が小さくなるため、多少選択肢より大きい値が出てもおかしくはありません。

以上より、正解は 3 です。