問 題
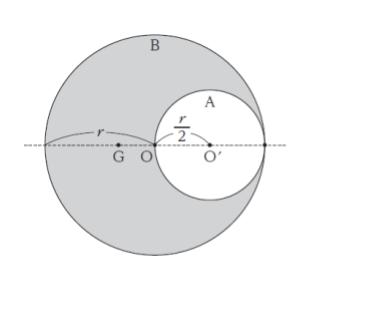
図のように、点 O を中心とする半径 r の一様な円板から、O より r/2 だけ離れた点 O’ を中心とする半径 r/2 の円板 A を切り抜き、残った板 B の重心を G とする。このとき、OG 間の距離として最も妥当なのはどれか。
正解 (2)
解 説
元の円板の面積を1とすれば、くり抜いた円板の面積は 1/4 です。するとくり抜いた円板を除いた太い三日月のような形の面積は 1-1/4 = 3/4 と表すことができます。
円の中心 O に指を立てて支えているイメージを考えます。すると、図の時には左に傾いていくのが想像できると思います。
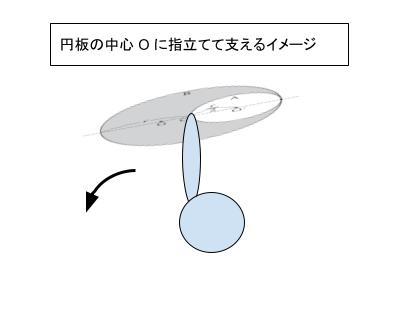
ここで、くり抜いた円盤をパコッとはめた場合を考えると、中心 O は元の円板の重心なので、指を立てて丁度支えられるはずです。重心に質量が下向きにかかると考え、模式的に表せば、以下のような図で表すことができます。
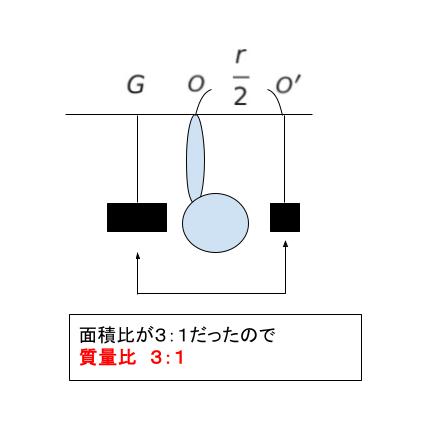
点 O からの距離は質量の逆比でつりあうので、GO:OO’=1:3です。OO’ は r/2 なので、OG は r/2 ÷ 3 = r/6 と表せます。
以上より、正解は 2 です。
類題 2019 no13 水平に静止した棒と重心
https://yaku-tik.com/koumuin/2019-gijyutu-13/

コメント