問 題
自然長Lの軽いばねの一端を天井に固定し、他端に小球をつるして静止させたところ、ばねの長さは 3/2 Lになった。
次に、同じ小球とばねを用いて、図のように、ばねが常に鉛直線と角θをなすように小球を水平面内で等速円運動させたとき、ばねの長さは2Lであった。
このとき、小球の速さとして最も妥当なのはどれか。
ただし、重力加速度の大きさをgとする。
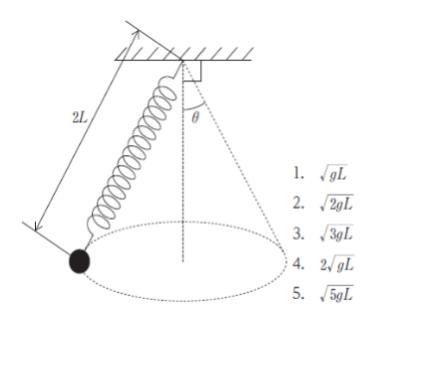
正解 (3)
解 説
等速円運動ときたので「F遠心力=mrω2=mv2/r」を思い出します。
まず、小球の質量を m とおき、下向きに mg の力がかかっているとします。
次にばねについて考えます。
ばねに普通に小球をつるしてmg の力がかかると、自然長 L のばねが3/2 L になったとあります。つまり、「mg で 1/2L 伸びて」います。
今、ばねの長さは 2L で自然長に比べて L 伸びていることから、「2mg の大きさ」だけばね方向に力がかかっていることがわかります。
以上より、力を書き込むと下図のようになります。
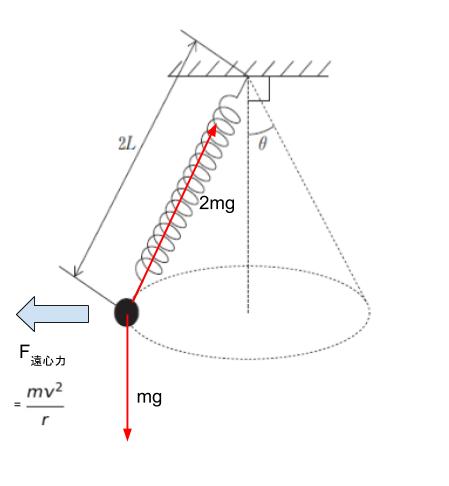
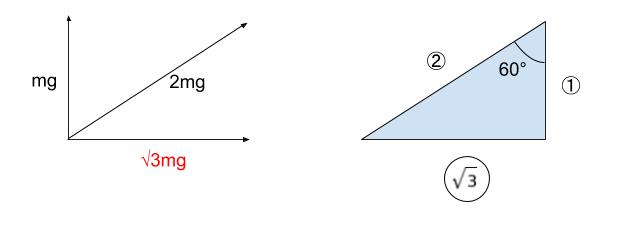
ばねの斜めの方向を縦と横に分解して考えます。
縦の力のつり合いを考えれば、ばね縦方向の力は mg です。
すると横が √3mg で、辺の長さが 1:2:√3 なので、θ = 60°とわかります。
※問題文の図が全然違うので図の見た感じとは一致しません。
また、これで等速円運動の半径は √3L とわかります。
横方向の力のつり合いに注目すれば
√3mg = mv2/√3L です。
m を消して両辺に√3かけると
3g = v2/L
∴ v2 = 3gL
∴ v = √3gL
以上より、正解は 3 です。
類題 H27no12

コメント