2020年 国家一般職(高卒 技術) No.21 電気基礎　解説

　問 題　　　　　

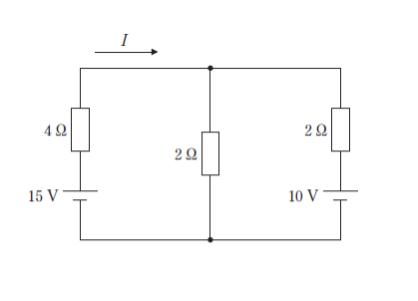
図のような回路において、電流 I の大きさはおよそいくらか。

1． 1 A
2． 2 A
3． 3 A
4． 4 A
5． 5 A

 

 

 

 

 

　解 説　　　　　

電池が 2 つ以上あるので、キルヒホッフの法則を思い出します。下図のように、I が分かれた後の電流を I₁、I₂ とします。キルヒホッフの電流則から 「I = I₁ + I₂」・・・（１） が成立します。

次に、キルヒホッフの電圧則より『起電力の和＝電圧降下の和』が、任意の閉回路で成立することを利用します。起電力は、電池をマイナス→プラスに横切る時に増え、逆の時は減ります。電圧降下は、各抵抗における R × I です。考えている閉回路の向きと電流の向きが同じ時は符号が正、逆の場合は符号が負です。

まず、左半分の閉回路に注目します。起電力の和は 15 です。電圧降下は 4 × I + ２ × I₂ です。15 = 4I + 2I₂ ・・・（２）という式を得ます。

同様に、右半分の閉回路に注目します。起電力の和は 10 です。電圧降下は ー 2I₁ + 2I₂  です。電流の向きと逆に抵抗を横切った際は、電圧降下の符号がマイナスになる点に注意します。10 = ー 2I₁ + 2I₂ ・・・（３）です。未知数が I,I₁,I₂ の３つで、式が３つできたので、解けます。

連立方程式を解いてもよいのですが、選択肢の活用がおすすめです。選択肢 1 が正解と仮定すると、I = 1 です。すると式（２）より I₂ = 5.5 です。（３）より I₁ = 0.5 です。しかしこれでは I = I₁ + I₂ が成立しません。従って、正解は 1 ではありません。

同様に検討すると、選択肢 2 が正解です。
I = 2 → I₂ = 3.5 → I₁ = -1.5 とわかります。

以上より、正解は 2 です。