問 題
図のように一様な弾性体で材質の異なる材料1、材料2からなる棒材の両端に剛体の板を付け、板を平行に保って両端を荷重Pで引っ張るとき、材料1の棒材に生じる軸方向応力度の大きさとして最も妥当なのはどれか。
ここで、材料1、材料2のヤング係数はE1、E2、それぞれの材料の断面積はA1、A2とする。
また、棒材の自重及び引っ張りに伴う断面積の変化は無視する。
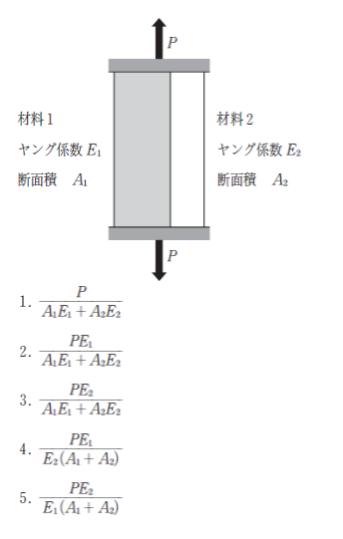
正解 (2)
解 説
【解法1】
ヤング率が出てきたら以下の3つの式を組合せて考えます。
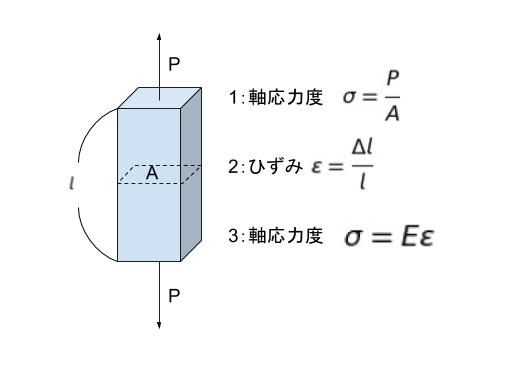
棒材の途中で切って考えます。材料1の部分も材料2の部分も伸び ε は同じと考えられます。
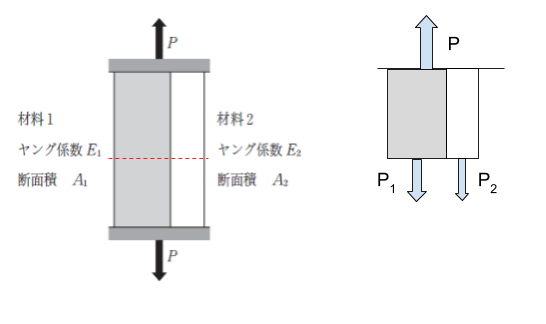
軸応力はそれぞれの部分において
- σ材料1 = E1ε
- σ材料2 = E2ε
と表せます。
軸応力に関する式1を上の式の左辺に代入すれば
- P1/A1 = E1ε ・・・(1)
- P2/A2 = E2ε ・・・(2)
です。
(1)の左辺が、正に求めたい材料1の棒材に生じる軸方向応力度の大きさです。
従って、選択肢に注目すれば、(1)の右辺を、 ε を使わずA2,E2、Pで表すことができれば答えということになります。
ここで縦方向の釣合に注目すれば、
- P1+P2=P・・・(3)
です。
(3)を(2)に代入してε = ・・・の形にしてから(1)に代入します。以下のようになります。

【解法 2 】
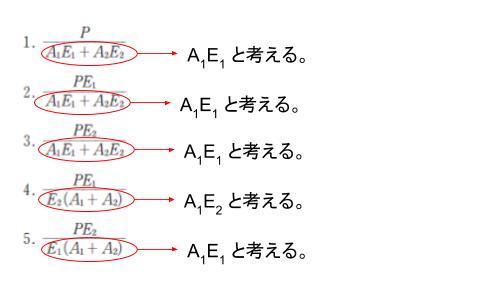
A1 がすごく大きい場合、ほぼP/A1 になるはず。
選択肢を検討すると
- P/A1E1
- P/A1
- PE2/A1E1
- PE1/E2A1
- PE2/E1A1
なので、P/A1 となる 選択肢 2 が正解です。

コメント