問 題
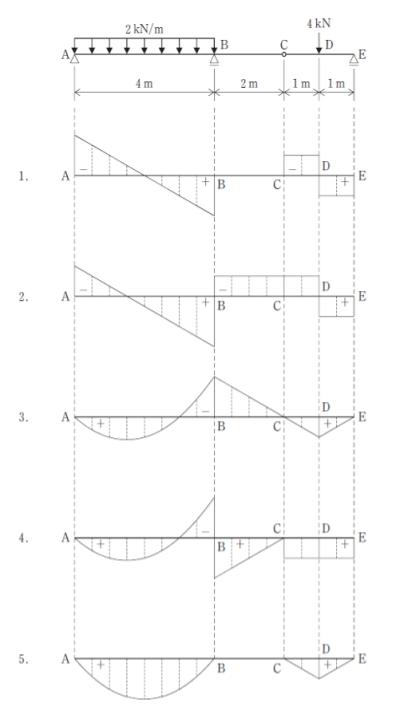
図のようにAB間に等分布荷重が作用し、点Dに集中荷重が作用しているゲルバー梁の曲げモーメント図の概形として最も妥当なのはどれか。
ただし梁の自重は無視する。
解 説
ゲルバー梁とは、「支点が3つ以上あり、かつ、途中にピン構造があって静定構造(=力の釣合だけで反力などがわかる構造)となっている梁」のことです。
ゲルバー梁が出てきたらピン構造の点で切断して考えるとよいです。まず反力を考えます。
【反力の計算】
C点で仮想切断し、より単純なので右側にまず注目すると、以下のようになります。
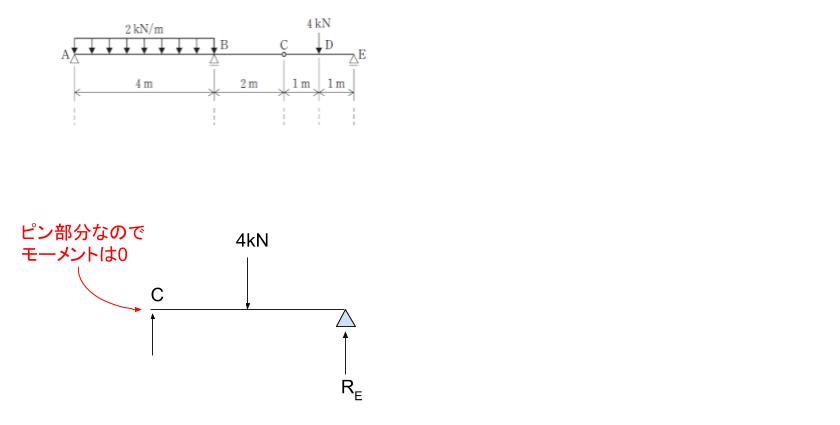
C点まわりのモーメントに注目すれば1 × 4 = 2 × RE です。∴RE = 2 kN です。
次に、縦方向の釣合に注目すれば、Cで切断した時の右側断面における上向きの力は 2kN とわかります。
次に、C点で仮想切断し左側に注目します。さきほど、C 点「右」側断面が↑2kN とわかっているので、C点「左」側断面に↓2kN の力がある点に注意します。
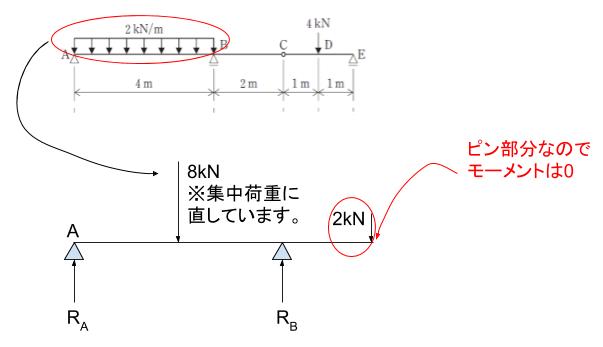
縦方向の力の釣合に注目するとRA+RB = 10 です。また A点まわりのモーメントに注目すれば2×8 + 6×2 = 4×RB →RB = 7 とわかります。RA+RB = 10 だったのでRA = 3 です。
以上で反力がわかりました。下図のようにまとめることができます。
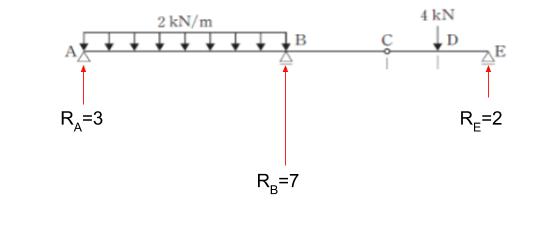
曲げモーメントについて、上図を見つつ考えます。力が単純なのでEからだんだん左に見ていきます。
【E~D に注目した曲げモーメント】
- 点EにおいてはM = 0 です。
- E~Dで切断して考えるとその点における曲げモーメントはDE間の距離×RE です。
つまり、E~Dの範囲では曲げモーメントの大きさはだんだん大きくなります。
以上より、正解は 3 or 5 にしぼられます。
【CB間に注目】
3 と 5 の違いは、CB 間においてずっと0かどうかなので、CBの中点(MBC)で切断して考えます。※1点に注目するとわかりやすいためです。
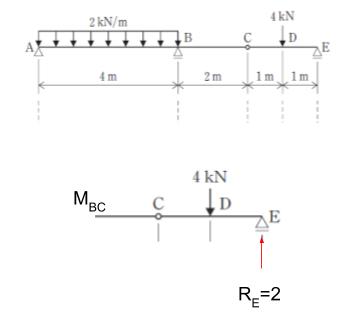
すると、点MBCにおけるモーメントをMとおけば 3×4=4× 2 + M です。M = 4 です。0 ではないため、明らかに 選択肢 5 は誤りです。
以上より、正解は 3 です。

コメント