問 題
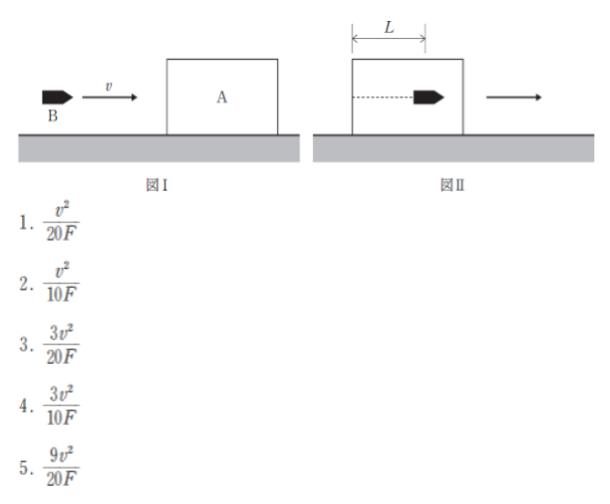
図Ⅰのように、水平かつ滑らかな床の上に置かれた質量9kgの物体Aに質量1kgの小物体Bを速さv〔m/s〕で打ち込んだところ、図Ⅱのように、BはAに距離L〔m〕だけ侵入し、侵入後はそのままAとともに運動した。
このとき、Lとして最も妥当なのはどれか。
ただし、BがAに侵入し続けている間は大きさ及び向きが一定の摩擦力F〔N〕が作用し、AとBは水平方向の一直線上を運動するものとする。
また、空気抵抗は無視できるものとする。
なお、BがAに侵入するときに減少する運動エネルギーは摩擦力がする仕事に等しい。
正解 (5)
解 説
物質の衝突→運動量保存を考えるというのが原則です。
図Ⅰの状態では動いているのは B で、質量 1, 速度 v だから運動量は v です。
図Ⅱの段階で一体となって動いている速度を V とおくと、質量は 1+9 = 10 なので運動量は 10V となります。
運動量は保存されるため v = 10V です。V = 1/10 v となります。
これだけでは L について何もわかりません。衝突で運動量を使って終わらなければ、運動エネルギーに注目するのが次の定石です。
図ⅠではK図Ⅰ= 1/2 v2 です。
図ⅡではK図Ⅱ = 1/2 × 10 × (1/10 v)2= 1/20 v2 です。
従って、1/2 v2 – 1/20 v2 = 9/20 v2 だけ運動エネルギーが減少しています。
この失われたエネルギーは仕事と同じ量です。仕事とは、力×距離です。(これは物理の基礎的知識です。)
本問では摩擦力が F で一定とあるので、FL = 9/20 v2 です。
従って、L = 9/20F v2 となります。
正解は 5 です。

コメント