問 題
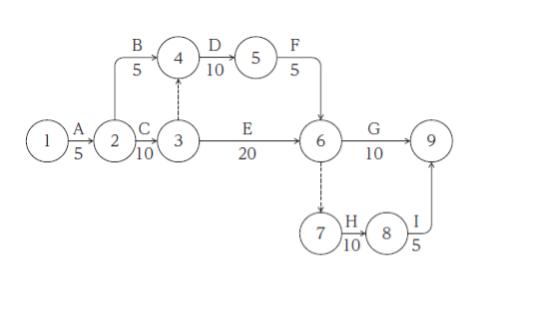
図のようなネットワーク式工程表で作業 A ~ I を実施するとき、クリティカルパスの所要日数として最も妥当なのはどれか。ただし、図中の矢印の下の数字は所要日数を、丸の中の数字は結合点番号を、破線はダミーをそれぞれ表している。
1.30 日
2.35 日
3.40 日
4.45 日
5.50 日
解 説
ネットワーク式工程表が出てきたら
・「最速時間」と「最遅時間」をそれぞれの段階に対し求める
→余裕時間(「最遅ー最速」)が0の所をつなぐ
→クリティカルパスが見つかる という流れが定石です。
「最速時間」は原則、左から右に向かって時間を足していけば OK です。この際、ある点に向かう経路が複数ある時、「遅い方の時間」を書き込むのが注意点です。まず、1通りしか行き方がない点までの最速時間を黒数字で書き込んだのが下図です。
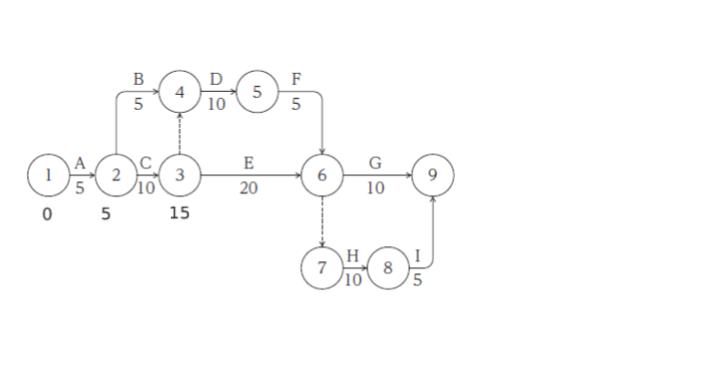
複数行き方がある点で「一番遅い時間」を赤字で加えたのが下図です。例えば結合点4までの経路として A → B で 10 でいける経路と A → C → ダミー で 15 かかる経路があります。遅い方が 15 なので赤で「15」となっています。
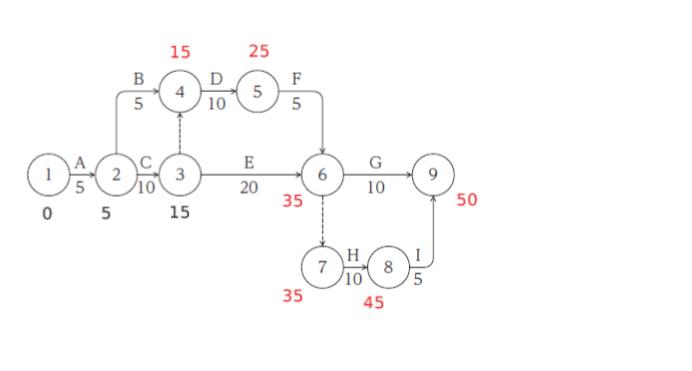
これで所要日数は 50日とわかります。
問題によって、クリティカルパスが聞かれるので、以下の最遅時間、クリティカルパスの発見まで ぜひ練習しておいてください。クリティカルパス発見のため、最遅経路を求めていきます。ゴールから逆にたどっていって、日数を引いていくのですが、複数ある場合は「小さくなる方」を選びます。既存の数値の下に 青色で加えたのが下図です。
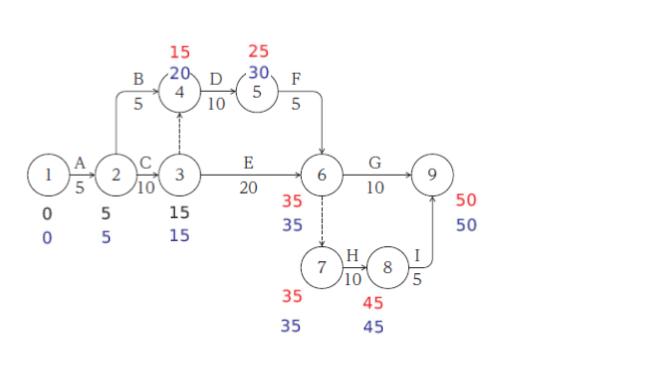
最遅ー最速=0となるのは「A → C → E → ダミー → H → I」です。これがクリティカルパスとなります。最遅ー最速を「余裕時間」といいます。
以上より、正解は 5 です。
類題 H28 no40 アローダイアグラム
https://yaku-tik.com/koumuin/h28-gijyutu-40/

コメント