問 題
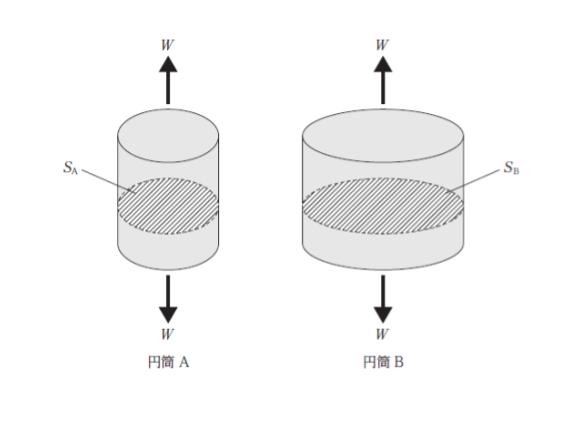
図のように、同じ材質の一様な円筒 A と円筒 B に荷重 W を円筒の軸方向に作用させる。軸に垂直な A の断面の断面積 SA と軸に垂直な B の断面の断面積 SB の間に、SB = 2SA の関係があるとき、A の断面にかかる応力 σA と、B の断面にかかる応力 σB の関係を表す式として最も妥当なのはどれか。ただし、A と B の自重は無視するものとする。
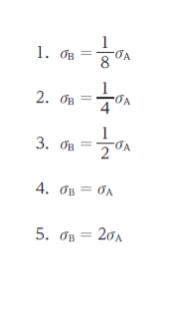
正解 (3)
解 説
軸方向力を P、断面積 A とすると、軸応力 σ は P/A です。これは基礎知識です。
δA = W/SA
δB = W/SB = W/2SA と表せます。
軸方向力が同じで、断面積 2 倍になっており、σB = σA/2 です。
以上より、正解は 3 です。
類題 2022 no52 棒に生じる引張応力の大きさ
https://yaku-tik.com/koumuin/2022-gijyutu-52/

コメント