問 題
曲線 y = -x3 -3x2 のグラフの概形として最も妥当なのはどれか。
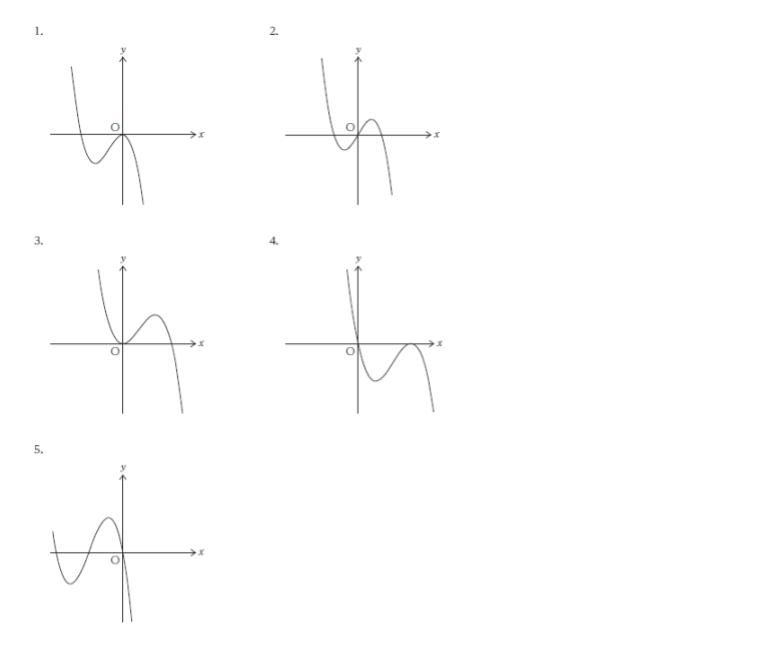
正解 (1)
解 説
解法1【y 軸との交点を 因数分解で求める】
y = -x3 -3x2 = -x2(x+3) です。
x 軸、つまり y = 0 との交点は x = 0 と x = -3 のみとわかります。従って、 x > 0 で交わったり、 x < 0 で 2個交わっている選択肢 2 ~ 5 は誤りです。
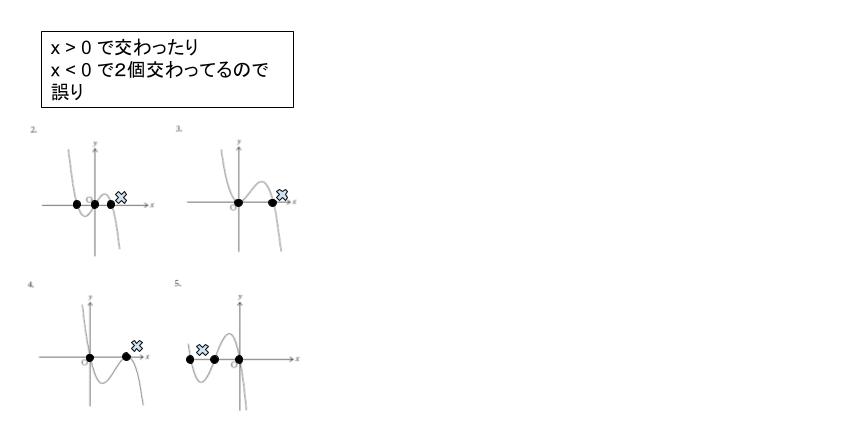
従って、正解は 1 です。
解法2【具体的な点で考える】
・x = 0 の時 0 は全ての選択肢が通っています。
・x = 0 よりも少しだけ右に進んだ時のグラフに注目します。選択肢 2,3 は y 座標が正となっています。そこで例えば x = 0.1 の場合の y の値を計算すると、y = -(0.1)3 -3(0.1)2 = -0.031 となり、負です。選択肢 2,3 は誤りです。
・x = 0 よりも少しだけ左に進んだ時のグラフに注目します。選択肢 4,5 は y 座標が負です。例えば x = – 0.1 の時、y = -(-0.1)3 -3(-0.1)2 = 0.029 となり正です。選択肢 4,5 は誤りです。
以上より、正解は 1 です。
類題 H29 no5 グラフの概形
https://yaku-tik.com/koumuin/h29-gijyutu-05/

コメント