問 題
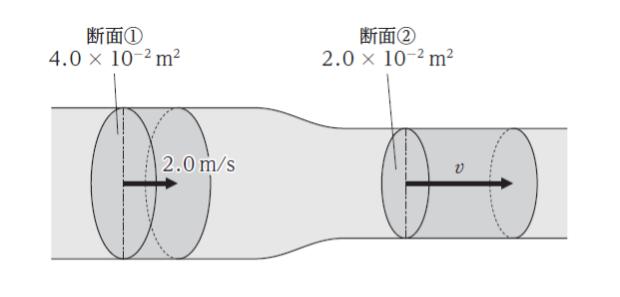
図のように、滑らかに断面積が変化する円管路を、一定流量の水が充満して定常的に流れている。
断面 ① における管路の断面積が 4.0 × 10-2 m2、水の流速が 2.0 m/s であり、断面 ② における管路の断面積が 2.0 × 10-2 m2 であるとき、断面 ② における流速 v として最も妥当なのはどれか。ただし、水は非圧縮非粘性流体とする。
1.1.0 m/s
2.2.0 m/s
3.4.0 m/s
4.6.0 m/s
5.8.0 m/s
正解 (3)
解 説
断面積の変化、問われているのが流速という点から、連続の式 Q = Av を思い出します。2つの断面において連続の式を用います。流量が一定なので「(4.0 × 10-2) × 2.0」=「(2.0 × 10-2) × v)」です。 選択肢の値を代入していけば、v = 4.0 です。
以上より、正解は 3 です。

コメント