問 題
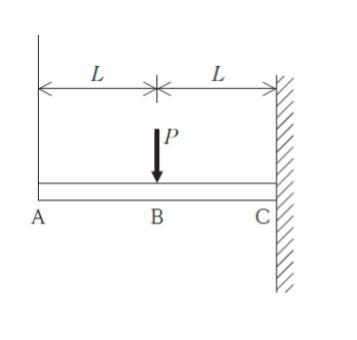
図のように、長さ 2L の一様な片持梁において、自由端 A と固定端 C の中間の位置 B に集中荷重 P が作用しているとき、梁に生じる曲げモーメントの大きさが最大となる位置として妥当なもののみを全て挙げているのはどれか。ただし、梁の自重は無視するものとする。
1.A
2.A、B
3.B
4.B、C
5.C
正解 (5)
解 説
【反力の計算】
まず反力を考えます。
・縦の力の和=0より
点 C において上向き、大きさ P の 反力 Rc が作用しています。
・横向き(軸方向)の力については作用していません。
・モーメントの和=0より
点 C 周りのモーメントを考えます。点 B に作用する下向き P の力により、反時計回り PL のモーメントがかかります。そのため、点 C において時計回り 大きさ PL のモーメント Mc が作用しています。
以上をまとめて図に書き込むと、以下のようになります。
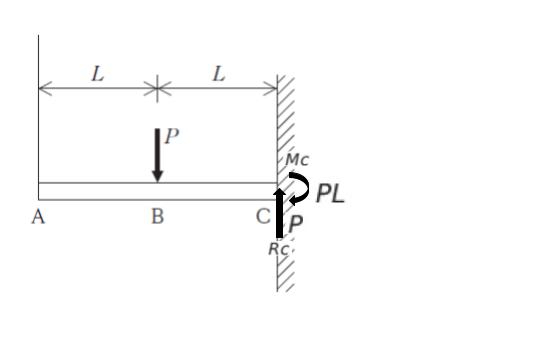
選択肢 を見ると
点 A,B,C の曲げモーメントのうち最大を見つける必要があります。
点 A に注目すると
点 A 周りのモーメントを考えれば、点 B における力 P による時計回りモーメント PL、点 C における反力 P による反時計回りモーメント 2PL、点 C における時計回りモーメント PL です。これらの和が0です。従って、MA = 0 です。
点 B に注目して
点 B で仮想切断します。左側の部材がわかりやすいと思われます。MB = 0 です。
点 C に注目すると
曲げモーメントは Mc = PL です。
以上より
曲げモーメントの大きさが最大である位置は C です。
正解は 5 です。

コメント