問 題
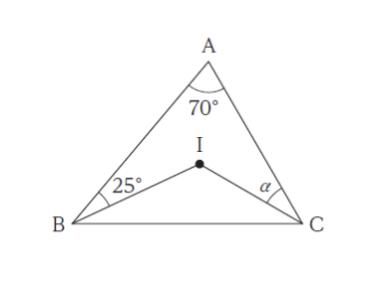
図のような △ABC において、点I が △ABC の内心で、∠BAC = 70°、∠ABI = 25°であり、∠ACI = α とするとき、α はいくらか。なお、三角形の内心は、三角形の三つの内角の二等分線が交わる点である。
1. 20°
2. 25°
3. 30°
4. 35°
5. 40°
正解 (3)
解 説
∠IBC = ◯、∠ICB = △ と表します。△ ABC に注目すると、∠A = 70° だから、∠ABC + ∠ACB = 180 – 70 = 110° です。

線分 BI、CI がそれぞれ角のニ等分線であるため、◯+△=110 ÷ 2 = 55° です。従って、△ BIC を見れば、∠ BIC = 180° ー 55° = 125° です。
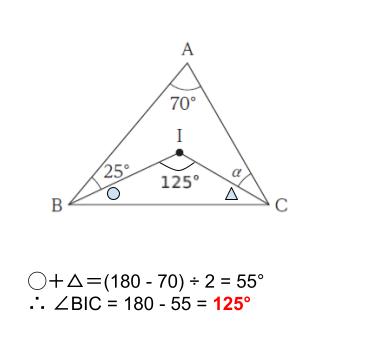
ブーメラン型(矢じり型、くさび型)ABIC において、3つの角の和(70° + 25° + α) は、溝部分の角度 125° です。これは求めることもできますが、むしろ基礎知識です。

従って、α = 30° です。
以上より、正解は 3 です。

コメント