問 題
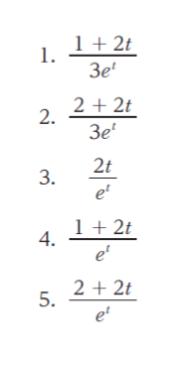
解 説
媒介変数 (パラメータ) 表示された関数です。dy/dx = (dy/dt)/(dx/dt) として計算するのが定石です。知らなかったり忘れた場合は「グラフの概形から判断」で選択肢を消去したい問題です。
【解法 1:媒介変数の微分】
(ex)’ = ex、(eax)’ = aeax
(xex)’ = ex + xex は基礎知識です。(積の微分、合成関数の微分について 類題参照)
dx/dt = 3e3t
dy/dt = e2t + 2te2t
dy/dx = e2t + 2te2t/3e3t
= (1+2t)/3et ※ 分母・分子を e2t で割っています。
以上より、正解は 1 です。
ーーー
【解法 2:グラフの概形を描き、選択肢を活用】
グラフの概形は「3 点見つけて滑らかにつなぐ」が基本です。e ≒ 2.7 は基礎知識です。
t = 0 の時、x(0) = e0 = 1、y(0) = 0 × e0 = 0 より
t = 0 の時、(1,0) を通ります。
t = 1 を考えると、かなり x 座標が大きくなる (e3 ≒ 20) ので
t = 1/3 を考えます。
t = 1/3 の時、x(1/3) = e1 ≒ 2.7、y(1/3) = 1/3 × e2/3 ≒ 2/3
t = 1/3 の時、(2.7、2/3) 付近を通ります。
※e2/3 は大雑把な評価をしています。
「3 乗したら e2 ≒ 7.3 になるような数 なので、e2/3 ≒ 2 としています。」
t = -1/3 の時、x(-1/3) = 1/e ≒ 1/3、y(-1/3) = -1/3 × e-2/3 ≒ -1/6
t = -1/3 の時、(1/3、-1/6) 付近を通ります。
従って
グラフの概形は以下のようになります。
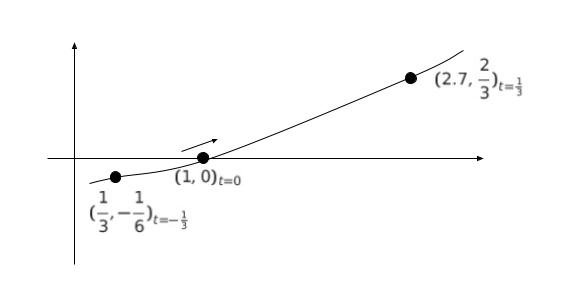
t = 0 前後において
グラフの傾きは緩やかな上昇傾向で、傾きは 1/2 よりも小さいと推測できます。
選択肢 に t = 0 を代入すると
1:1/3
2:2/3
3:0
4:1
5:2 です。
まず、明らかに 傾き 0 ではありません。選択肢 3 は誤りです。そして、1/2 よりも小さいのは選択肢 1 です。
以上より、正解は 1 です。
類題
国家一般職 高卒技術 H26 no5
https://yaku-tik.com/koumuin/h26-gijyutu-05/

コメント