2021年 国家一般職(高卒 技術) No.21 電気基礎　解説

　問 題　　　　　

図のような回路において、電流 I の大きさはおよそいくらか。

1．2 A
2．4 A
3．6 A
4．8 A
5．10 A

 

 

 

 

 

　解 説　　　　　

電池が 2 つ以上あるので、キルヒホッフの法則を思い出します。まず、電流則より I の流れる先の電流を I₁、I₂ とおけば、I = I₁ + I₂ が成立します。

左端の閉回路（時計回り）に注目します。キルヒホッフの電圧則より『起電力の和＝電圧降下の和』です。

電池を横切る符号に注意します。注目している回路の向きで進んでいった時に、電池をプラスからマイナスに横切った場合は、符号を負と読みます。従って、起電力の和は 10 ー 2 = 8 です。電圧降下は 4 Ω の抵抗部分において ４× I₁ です。従って、8 = 4 I₁ ∴ I₁ = 2 とわかります。

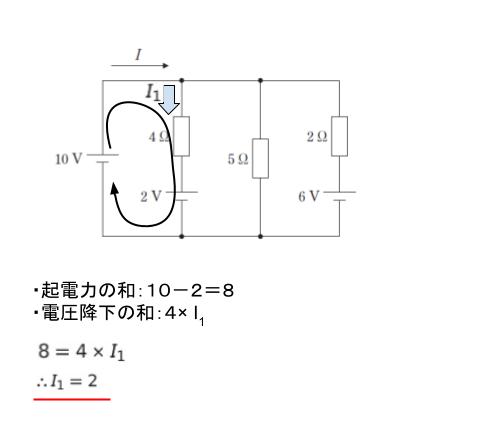
次に、I₂ の流れる先を I₃、I₄ とおきます。I₂ = I₃ + I₄ です。そして、大外時計回りの閉回路に注目すれば、起電力の和が １０－６＝４、電圧降下の和が 2 × I₄ です。これにより、I₄ = 2 とわかります。

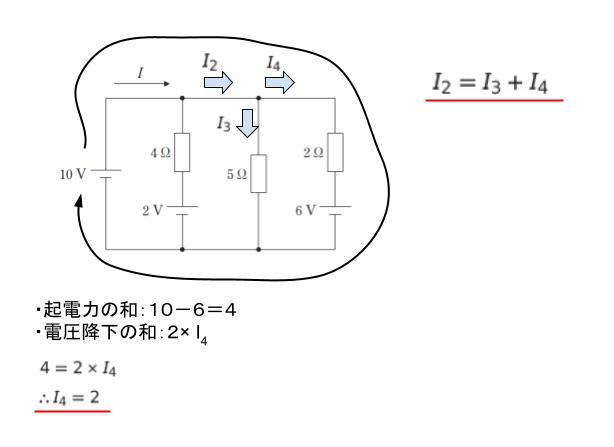
最後に右端の閉回路（反時計回り）に注目します。起電力の和が６です。電圧降下の和について、I₄ = 2 とわかっており、注目する回路の向きと I₄ の向きが逆である点に注意します。－４＋５I₃ が電圧降下の和です。６＝－４＋５I₃ より、I₃ = ２です。

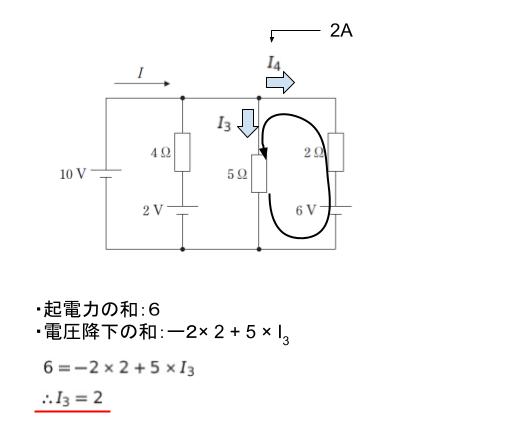
後は、電流を求めていきます。
I₂ = 2 + 2 = 4 です。従って、I = 2 + 4 = 6 とわかります。

以上より、正解は 3 です。