2021年 国家一般職(電気・電子・情報) No.27解説

　問 題　　　　　

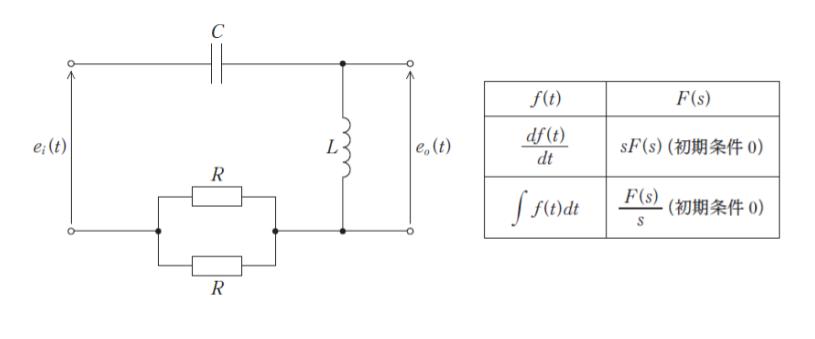
図のような RLC 回路において、入力電圧 e_i(t) と出力電圧 e_o(t) の関係を示す伝達関数 G(s) として最も妥当なのはどれか。

なお、表はラプラス変換表であり、e_i(t)、e_o(t) のラプラス変換をそれぞれ、E_i(s)、E_o(s) とするとき、伝達関数 G(s) = E_o(s)/E_i(s) である。

 

 

 

 

 

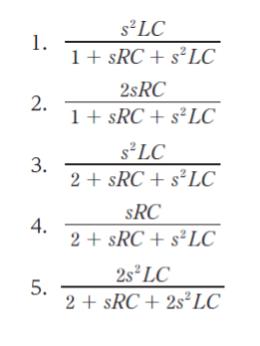
　解 説　　　　　

※回路方程式を解かないといけない問題ですが、このレベルの問題は出題頻度が低く、試験合格には不要です。深入りしないように気をつけてください！

R,L,C における電圧降下は、それぞれ流れる電流を i(t) として、Ri(t)、L(di(t)/dt)、1/C × ∫ i(t) dt です。これは基礎知識です。

本問において、R 2 つの並列回路は合成して、R/2 とします。以下の図のように合成した抵抗を 1 つにまとめた上で、電流 i(t) が C,L,R/2 に流れるとします。

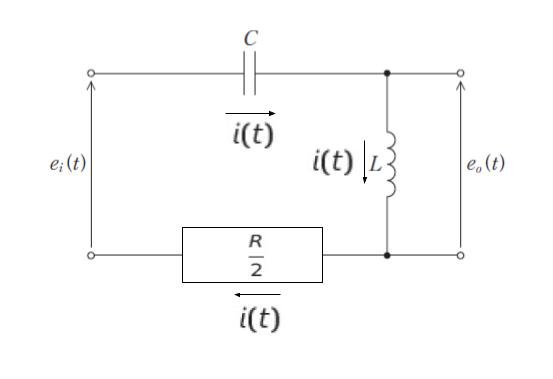
電圧降下に注目すれば、以下のような 2 つの式をたてることができます。

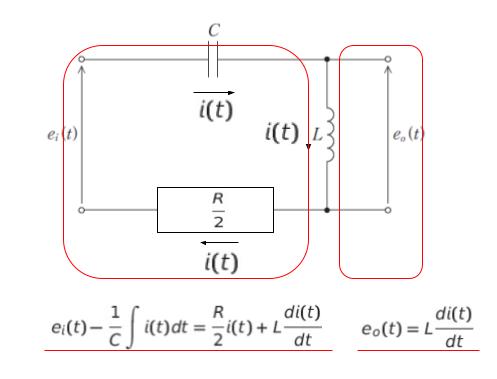
図の下、左側の式より
e_i (t) = (R/2) × i(t) + L(di (t)/dt)+ 1/C × ∫ i (t) dt です。

i (t) = f (t) として ラプラス変換すれば
L(e_i (t))
= (R/2) × F(s) + sLF(s) + (1/Cs) × F(s)
= F(s) × (R/2 + sL + 1/Cs) です。

一方、図の下、右側の式より
e_o (t) = L(di (t)/dt) です。

やはり i (t) = f (t) として ラプラス変換すれば
L(e_o(t)) = F(s) × sL です。

つまり
G (s) = (F(s) × sL)/{F(s) × (R/2 + sL + 1/Cs)}です。

F(s) が約分できて
G (s) = sL/ (R/2 + sL + 1/Cs) です。分母・分子に 2Cs をかけると
2s²LC/(2 + sRC + 2s²LC) と表せます。

以上より、正解は 5 です。

類題 H25 no27 RLC 回路
https://yaku-tik.com/koumuin/h25-denjyou-27/