問 題
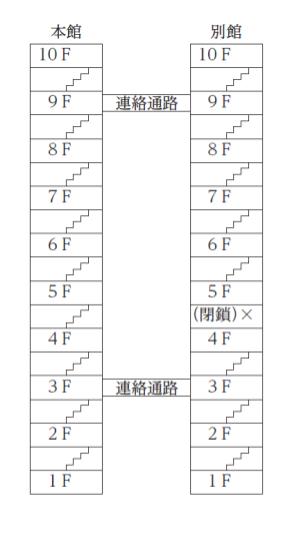
図のように,共に1 階~10 階まである本館と別館から成るホテルがある。ホテルの各階は階段でつながっており,本館と別館の3 階どうし, 9 階どうしをつなぐ連絡通路があるが,現在,別館の4 階と5 階をつなぐ階段が閉鎖されている。
本館の互いに異なる階にいるA~Eの5 人の従業員は,階段と連絡通路のみを使って,最短経路で別館の互いに異なる階に移動した。次のことが分かっているとき,確実にいえるのはどれか。ただし,階段の数は, 1 階と 2 階のように,上下の階をつなぐものを1 階段と数えるものとする。
〇 Aが使った階段の数の合計は,ホテルの本館から別館への移動としてあり得る中で最も多いものであった。
〇 Bが使った階段の数は,上りも下りも共に3 階段分であった。
〇 Cは上り階段も下り階段も使ったが,上り階段の数は下り階段の数の 3 倍であった。
〇 D が移動前にいた階とCが移動後にいた階は同じ階であったが,DはCよりも使った下り階段の数が3 階段分多かった。
〇 Eが使った階段は本館も別館も下りで,その数は合計で 3 階段分であった。
1.Aは,本館の 10 階から移動した。
2.Bは,別館の 5 階に移動した。
3.Cは,本館の 4 階から移動した。
4.Dは,別館の 8 階に移動した。
5.Eは,別館の 1 階に移動した。
解 説
箇条書きの条件を上から読み解いていきます。
「本館から別館への移動に必要な階段の数」は、1F からなら 2階段、2F からなら 1 階段・・・と考えていけば、6F からの3階段が最大です。従って、A が使った階段の数の合計は 3 階段です。
B は使った階段数が上りも下りも3階段分なので、本館6F にいたとわかります。そして、本館でまず下ったとすれば、本館 6F → 本館 3F → 別館 3F となりますが、別館の 4-5 間が封鎖されているため、ありえません。従って、「本館 6F → 本館 9F → 別館 9F → 別館 6F」 と B は移動したとわかります。
次に C ですが、上り階段の数が3の倍数なので、最低 3 階段分です。すると、別館9F からも 別館 3F からも3階段上がるのはありえないため、別館で上っていません。C は、別館で「下った」と考えられます。
そして、上り3階段ならば、元居た階は本館 6F となりますが、本館 6F は B が居た階です。上り3階段はありえません。また、最短経路で上り9階段はありえません。従って、上り6階段です。これにより、下り2階段とわかります。すると、「本館3F → 本館 9F → 別館 9F → 別館 7F」 と C は移動したとわかります。
D は、C の移動後にいた階である「7階」にいて、C より3階段分多い「5階段下った」ということなので、「本館7F → 本館 3F → 別館 3F → 別館 2F」 と D は移動したとわかります。
E は下り階段のみを、合計3階段分使ったということなので、1:本館 10F → 9F → 別館7F、2:本館 6F → 3F、3:本館 5F → 別館2F 、4:本館4F → 別館 1F が考えられます。1は到達地が C とかぶってだめです。2はスタートが B とかぶってだめです。3は D と到達地がかぶってだめです。従って、本館 4F → 本館 3F → 別館 3F → 別館 1F と確定します。
だいぶきまったので、選択肢を検討します。
選択肢 1 ですが
本館 10 F からだと、10 → 9 → 別館 7 F となり、到着階が C とかぶってだめです。選択肢 1 は誤りです。
選択肢 2 ですが
B は別館の 6F に移動しました。5F ではありません。選択肢 2 は誤りです。
選択肢 3 ですが
C は本館の 3F から移動しています。4F ではありません。選択肢 3 は誤りです。
選択肢 4 ですが
D は別館の 2F に移動しました。8F ではありません。選択肢 4 は誤りです。
以上より、正解は 5 です。

コメント