問 題
企業Aは,企業Bが独占している市場に新規参入すべきか検討しており,以下のゲーム・ツリーで表される展開型ゲームを考える。Aが「不参入」を選べば,Aの利得は 0 ,独占を維持できるBの利得は 8 である。また,Aが「参入」を選んだ場合は,Bが協調路線をとれば A の利得が 3 でBの利得が 4 になり,BがAに対抗して価格競争を仕掛ければAの利得が -2 でBの利得が 0 になる。この展開型ゲームについて,戦略型ゲームによるナッシュ均衡と部分ゲーム完全均衡を考える。次の記述のうち,妥当なのはどれか。ただし,純粋戦略を考えるものとする。

1.戦略型ゲームによるナッシュ均衡は存在しない。部分ゲーム完全均衡は「Aは参入,Bは協調」のみである。
2.戦略型ゲームによるナッシュ均衡は「Aは参入,Bは協調」のみである。部分ゲーム完全均衡は存在しない。
3.戦略型ゲームによるナッシュ均衡は「Aは参入,Bは協調」のみである。部分ゲーム完全均衡は「Aは参入,Bは協調」のみである。
4.戦略型ゲームによるナッシュ均衡は「Aは参入,Bは協調」のみである。部分ゲーム完全均衡は「Aは不参入,Bは対抗」と「Aは参入,Bは協調」である。
5.戦略型ゲームによるナッシュ均衡は「Aは不参入,Bは対抗」と「Aは参入,Bは協調」である。部分ゲーム完全均衡は「Aは参入,Bは協調」のみである。
解 説
ナッシュ均衡とは、全てのプレーヤーが、現在の戦略を変更すると、利得が今よりも増えないような状態です。(H30no35)。本問において、利得行列(各プレーヤーが取る戦略と、利得を表にしたもの)は、以下になります。
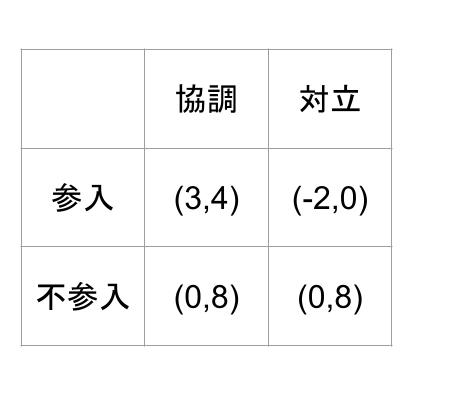
すると、「参入、協調」を選び、利得が (3,4)の場合、A が不算入にすると A の利得が 3 → 0、B が対立にすると B の利得が 4 → 0 となるため、共に利得が今より増えません。ナッシュ均衡です。
また、「不参入、対立」を選び、利得が (0,8) の場合、A が参入にすると A の利得が 0 → -2、B が協調にすると B の利得が 0 → 0 なので、やはり共に利得が今より増えません。こちらもナッシュ均衡です。
部分ゲーム完全均衡とは、多期間におけるゲームのどの部分においてもナッシュ均衡が成立している状態のことです。ゲームの最終段階から、後ろ向きにゲームをたどっていくことで見つけることができます。本問であれば、ゲームの枝を右端から見ると、まず、B が協調をとるのが合理的です。B が合理的をとるのであれば、A は参入を選ぶのが合理的です。従って、A 参入、B 協調 の組み合わせが、部分ゲーム完全均衡です。
以上より、正解は 5 です。

コメント