問 題
財 1 ,財 2 の二つの財を消費する消費者の効用関数が
u = x12x23(u:効用水準,x1:財1 の消費量,x2:財2 の消費量)
で与えられている。
また,この消費者は,財 1 の価格が p1( > 0),財 2 の価格が p2( > 0),所得が I の下で,効用を最大化しているものとする。このとき,この消費者と同じ効用関数を持つ消費者が 100 人いたときの市場全体の財 1 の需要関数として妥当なのはどれか。ただし,X1 は市場全体の需要量であるとする。
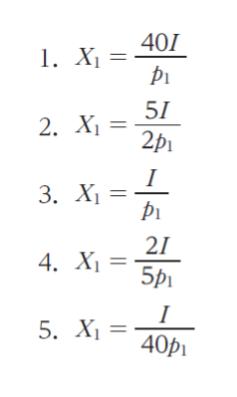
解 説
予算制約を p1x1 + p2x2 = I として、前問 no31 と同様に計算すると一応解けるのですが、計算がとても複雑になり現実的な解き方ではありません。p1 = p2 = I = 1 のように具体的におくと、ぎりぎり現実味のある計算量になります。(別解1)。また、制約条件下での効用最大化について、ラグランジェの未定係数法で計算するのも、ありだと思います。(別解2)。計算力で解き切る練習もしておくとよいです。
計算にあまり頼らない方法として、効用関数が「コブ・ダグラス型: u = AKαLβ (K,L が変数、他は定数。本問では、A = 1、α = 2、β = 3) 」であることに注目します。この時、効用最大化が成立するのが「2財に対して所得を α:β に分配した時」という知識を使います。(これを知らなかった人は、ぜひこの機会に覚えておきましょう。)。ここで更に I = 10 のように具体的、かつ、5で割れる数にしておくとわかりやすいです。I = 10 とすれば、効用最大化成立時、所得を2:3に分配すると、財1に対して所得を 4、財2に対して所得を6使うということになります。
具体的な財1、財2の消費量 x1,x2 を考える時に、p1 や p2 で割る必要があります。文字のままだとわかりにくいので、これも p1 = p2 = 1 のように具体的に勝手に決めてしまうと考えやすいです。公務員試験では「変数は具体的数で考える」は一般的に役立つ戦術となります。
x1 = 4 ÷ 1 = 4、x2 = 6 ÷ 1 = 6 となります。従って、財1 の需要量は 4 です。消費者が 100 人いるので、市場全体の需要量は 400 です。
需要関数に具体的値を代入すれば、ある条件における需要量がわかるのだから、今回勝手に設定した p1 = 1、I = 10 を代入した時に 400 になる式が正解です。X1 = 40I/p1 とわかります。
以上より、正解は 1 です。
以下、別解1,2です。
別解1【p1 = p2 = I = 1 と勝手に設定し、前問 no31 と同様に微分】
所得が 1 なので、x1 + x2 = 1 ・・・(1) 。x1 = 1 – x2 を代入し、効用関数を「2文字の式」→「1文字の式」にします。u = (1 – x2)2 x23 と表せます。
u’ = 5 x24 -8x23 +3x22 = x22(5x22 – 8x2 +3) = x22(5x2 – 3)(x2 -1) なので、u’ = 0 となるのは、x2 = 3/5 の時です。(1)に代入して、x1 = 2/5 とわかります。 2/5 × 100 = 40 です。
今回勝手に設定した p1 = 1、I = 1 を代入した時に 40 になる式が正解です。X1 = 40I/p1 とわかります。
別解2【ラグランジュの未定係数法 で計算】
「効用関数が複雑で、『自然な代入 → 微分』が難しい場合」に試みる方法です。具体的な解き方は、以下のように 3 step となります。
step1:予算制約式の右辺が 0 になるように式変形
p1 = p2 = I = 1 と設定した場合であれば x1 + x2 -1 = 0 という式変形を行うということです。
step2:ラグランジュ式と呼ばれる L(x,y,λ)を作成
L(x,y,λ)= u – λ(変形した予算制約式の左辺) です。本問であれば、u = x12x23、変形した予算制約式の左辺が x1 + x2 -1 なので、L(x1,x2,λ) = x12x23-λ(x1 + x2 -1) です。
step3:3つの変数で偏微分した式を計算し、= 0 を取り付けて、3 つの式を作ります。連立して解けば終わりです。この過程を経て出てきた x1,x2 が、効用最大化時における財の消費量となります。λ は気にしなくて OK です。赤文字部分が注目している変数です。
dL/dx1 = 0 ↔ 2x23 x1 – λ = 0
dL/dx2 = 0 ↔ 3x12x22 – λ = 0
dL/dλ = 0 ↔ 1 – x1 – x2 = 0
上2つの式から λ を消去すると 2x23 x1 = 3x12x22 ∴ 3x1 = 2x2
一番下の式と連立すれば、x1 = 2/5 を得ます。

コメント