問 題
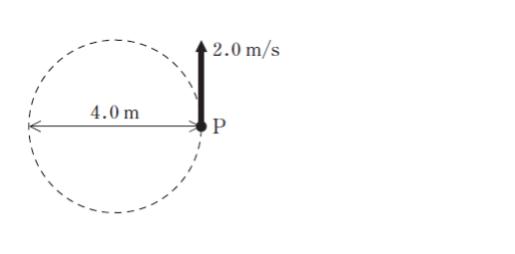
図のように、質点 P が、直径 4.0 m の円周上を速さ 2.0 m/s で等速円運動するとき、この円運動の周期はおよそいくらか。ただし、円周率を 3.1 とする。
1．3.1 s
2．4.7 s
3．6.2 s
4．7.8 s
5．9.3 s
正解 (2)
解 説
【解法１：速さの問題として道のり ÷ 速さで解く】
直径 4.0 m の円の円周は 4.0 Π です。円周率が 3.1 なので 12.4 m です。
円運動の周期とは、１周するのにかかる時間のことです。時間＝道のり ÷ 速さ なので、12.4 ÷ 2.0 = 6.2 秒です。
以上より、正解は 2 です。
【解法２：円運動なので、単位ラジアンの角速度を考える】
等速円運動の速さの公式 v = r ω を思い出します。v = 2.0、r は半径なので、直径の半分だから 4.0 ÷ 2 = 2.0 m です。これにより、角速度 ω = 1（ラジアン）です。
円１周は 2 Π ラジアンです。これは基礎知識です。１周するのに 2 Π 秒 かかります。つまり、 2 × 3.1 = 6.2 秒かかります。
以上より、正解は 2 です。
コメント