問 題
赤玉 4 個と白玉 2 個の計 6 個が入っている袋から、同時に 2 個の玉を無作為に取り出すとき、少なくとも 1 個は白玉である確率はいくらか。
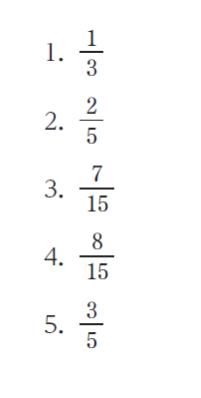
正解 (5)
解 説
確率の定義は「該当する通り/全ての通り」です。これは基礎知識です。(参考 高卒基礎 H30 no15 合計 10 個の玉から同時に 3 個取り出す問題)。
本問において全ての通りは「玉 6 個から 2 個取り出した通り」です。 6C2 と表せます。該当する通りは「赤2個」の通りを「全ての通りから引く」ことで求めることができます。「赤2個」の通りは 4C2 と表せます。従って、求める確率は以下のように表されます。
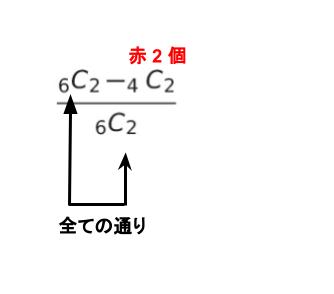
・6C2 = 6!/2!4! = 6×5/2×1 = 15
・4C2 = 4!/2!2! = 4×3/2×1 = 6 です。
代入して計算すると
(15-6)/15 = 9/15 = 3/5 です。
以上より、正解は 5 です。

コメント